题目内容
【题目】设函数 
，若函数 
在 
处与直线 
相切．
（Ⅰ）求实数 
的值；
（Ⅱ）求函数 在 
上的最大值．
【答案】解：(Ⅰ)f′(x)＝ 
－2bx ， ∵函数f(x)在x＝1处与直线y＝－ 
相切，
∴ 
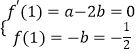解得 
(Ⅱ)由(1)知， 
， 
当 
≤x≤e时，令f′(x)>0，得 ≤x<1，
令f′(x)<0，得1<x≤e， ∴f(x)在[ ，1)上是增加的，
在(1，e]上是减少的， ∴f(x)max＝f(1)＝－ .
【解析】本题主要考查导数的几何意义和利用导数求解最值问题。第一小题主要利用导数的几何意义，根据函数与直线相切，可得直线
是函数在
处的切线，列出方程组即可。第二小题直接根据函数求导，利用导数求出函数的单调区间，根据单调性求出区间上的最大值。
【考点精析】认真审题，首先需要了解导数的几何意义(通过图像,我们可以看出当点
趋近于
时，直线
与曲线相切．容易知道，割线
的斜率是
，当点趋近于时，函数
在
处的导数就是切线PT的斜率k，即
)，还要掌握函数的最大(小)值与导数(求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值)的相关知识才是答题的关键．
练习册系列答案
相关题目
