ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌгЮПЭДгФГТУгЮОАЧјЕФОАЕу![]() ДІЯТЩЯжС
ДІЯТЩЯжС![]() ДІгаСНжжТЗОЖЃЎвЛжжЪЧДг
ДІгаСНжжТЗОЖЃЎвЛжжЪЧДг![]() бижБЯпВНааЕН
бижБЯпВНааЕН![]() ЃЌСэвЛжжЪЧЯШДг
ЃЌСэвЛжжЪЧЯШДг![]() биЫїЕРГЫРТГЕЕН
биЫїЕРГЫРТГЕЕН![]() ЃЌШЛКѓДг
ЃЌШЛКѓДг![]() бижБЯпВНааЕН
бижБЯпВНааЕН![]() ЃЎЯжгаМзЁЂввСНЮЛгЮПЭДг
ЃЎЯжгаМзЁЂввСНЮЛгЮПЭДг![]() ДІЯТЩНЃЌМзби
ДІЯТЩНЃЌМзби![]() дШЫйВНааЃЌЫйЖШЮЊ
дШЫйВНааЃЌЫйЖШЮЊ![]() ЃЎдкМзГіЗЂ
ЃЎдкМзГіЗЂ![]() КѓЃЌввДг
КѓЃЌввДг![]() ГЫРТГЕЕН
ГЫРТГЕЕН![]() ЃЌдк
ЃЌдк![]() ДІЭЃСє
ДІЭЃСє![]() КѓЃЌдйДг
КѓЃЌдйДг![]() дШЫйВНааЕН
дШЫйВНааЕН![]() ЃЌМйЩшРТГЕдШЫйжБЯпдЫЖЏЕФЫйЖШЮЊ
ЃЌМйЩшРТГЕдШЫйжБЯпдЫЖЏЕФЫйЖШЮЊ![]() ЃЌЩНТЗ
ЃЌЩНТЗ![]() ГЄЮЊ1260
ГЄЮЊ1260![]() ЃЌОВтСП
ЃЌОВтСП![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
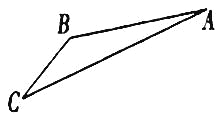
ЃЈ1ЃЉЧѓЫїЕР![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉЮЪЃКввГіЗЂЖрЩй![]() КѓЃЌввдкРТГЕЩЯгыМзЕФОрРызюЖЬЃП
КѓЃЌввдкРТГЕЩЯгыМзЕФОрРызюЖЬЃП
ЃЈ3ЃЉЮЊЪЙСНЮЛгЮПЭдк![]() ДІЛЅЯрЕШД§ЕФЪБМфВЛГЌЙ§
ДІЛЅЯрЕШД§ЕФЪБМфВЛГЌЙ§![]() ЃЌввВНааЕФЫйЖШгІПижЦдкЪВУДЗЖЮЇФкЃП
ЃЌввВНааЕФЫйЖШгІПижЦдкЪВУДЗЖЮЇФкЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() m ЃЈ2ЃЉ
m ЃЈ2ЃЉ![]() ЃЈ3ЃЉ
ЃЈ3ЃЉ![]() ЃЈЕЅЮЛЃКm/minЃЉ
ЃЈЕЅЮЛЃКm/minЃЉ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнСННЧКЭЙЋЪНЧѓЕУ![]() ЃЌдйИљОне§ЯвЖЈРэМДПЩЧѓЕУ
ЃЌдйИљОне§ЯвЖЈРэМДПЩЧѓЕУ![]() ЕФГЄЃЛЃЈ2ЃЉМйЩшввГіЗЂ
ЕФГЄЃЛЃЈ2ЃЉМйЩшввГіЗЂ![]() КѓЃЌМзЁЂввСНгЮПЭОрРыЮЊ
КѓЃЌМзЁЂввСНгЮПЭОрРыЮЊ![]() ЃЌЗжБ№БэЪОГіМзЁЂввЖўШЫаазпЕФОрРыЃЌИљОнгрЯвЖЈРэНЈСЂ
ЃЌЗжБ№БэЪОГіМзЁЂввЖўШЫаазпЕФОрРыЃЌИљОнгрЯвЖЈРэНЈСЂ![]() ЕФЖўДЮКЏЪ§ЙиЯЕЃЌЧѓГіЪЙЕУМзввЖўШЫОрРызюЖЬЪБ
ЕФЖўДЮКЏЪ§ЙиЯЕЃЌЧѓГіЪЙЕУМзввЖўШЫОрРызюЖЬЪБ![]() ЕФжЕЃЛЃЈ3ЃЉИљОне§ЯвЖЈРэЧѓЕУ
ЕФжЕЃЛЃЈ3ЃЉИљОне§ЯвЖЈРэЧѓЕУ![]() ,ввДг
,ввДг![]() ГіЗЂЪБЃЌМзвбзпСЫ
ГіЗЂЪБЃЌМзвбзпСЫ![]()
![]() ЃЌЛЙашзп
ЃЌЛЙашзп![]()
![]() ВХФмЕНДя
ВХФмЕНДя![]() ,ЩшввВНааЕФЫйЖШЮЊ
,ЩшввВНааЕФЫйЖШЮЊ![]() ЃЌгЩЬтвтЕУ
ЃЌгЩЬтвтЕУ![]() ,НтВЛЕШЪНМДПЩЧѓЕУввВНааЫйЖШЕФЗЖЮЇ.
,НтВЛЕШЪНМДПЩЧѓЕУввВНааЫйЖШЕФЗЖЮЇ.
ЪдЬтНтЮіЃКЃЈ1ЃЉдк![]() жаЃЌвђЮЊ
жаЃЌвђЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ДгЖј![]()
![]()
![]() ЃЎ
ЃЎ
гЩе§ЯвЖЈРэ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЈ
ЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ2ЃЉМйЩшввГіЗЂ![]() КѓЃЌМзЁЂввСНгЮПЭОрРыЮЊ
КѓЃЌМзЁЂввСНгЮПЭОрРыЮЊ![]() ЃЌДЫЪБЃЌМзаазпСЫ
ЃЌДЫЪБЃЌМзаазпСЫ![]() ЃЌввОрРы
ЃЌввОрРы![]() ДІ
ДІ![]()
![]() ЃЌ
ЃЌ
ЫљвдгЩгрЯвЖЈРэЕУ![]()
![]() ЃЌ
ЃЌ
гЩгк![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЙЪЕБ![]() ЪБЃЌМзЁЂввСНгЮПЭОрРызюЖЬЃЎ
ЪБЃЌМзЁЂввСНгЮПЭОрРызюЖЬЃЎ
ЃЈ3ЃЉгЩе§ЯвЖЈРэ![]() ЃЌ
ЃЌ
ЕУ![]() ЃЈ
ЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
ввДг![]() ГіЗЂЪБЃЌМзвбзпСЫ
ГіЗЂЪБЃЌМзвбзпСЫ![]() ЃЈ
ЃЈ![]() ЃЉЃЌЛЙашзп710
ЃЉЃЌЛЙашзп710![]() ВХФмЕНДя
ВХФмЕНДя![]() ЃЎ
ЃЎ
ЩшввВНааЕФЫйЖШЮЊ![]() ЃЌгЩЬтвтЕУ
ЃЌгЩЬтвтЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЫљвдЮЊЪЙСНЮЛгЮПЭдк![]() ДІЛЅЯрЕШД§ЕФЪБМфВЛГЌЙ§
ДІЛЅЯрЕШД§ЕФЪБМфВЛГЌЙ§![]() ЃЌввВНааЕФЫйЖШгІПижЦдк
ЃЌввВНааЕФЫйЖШгІПижЦдк![]() ЃЈЕЅЮЛЃК
ЃЈЕЅЮЛЃК![]() ЃЉЗЖЮЇФкЃЎ
ЃЉЗЖЮЇФкЃЎ

ЁОЬтФПЁПЮЊСЫНтЩйФъЖљЭЏЕФЗЪХжЪЧЗёгыГЃКШЬМЫсвћСЯгаЙиЃЌЯжЖд30УћСљФъМЖбЇЩњНјааСЫЮЪОэЕїВщЃЌЕУЕНШчЯТСаСЊБэЃЈЦНОљУПЬьКШ500mlвдЩЯЮЊГЃКШЃЌЬхжиГЌЙ§50kgЮЊЗЪХжЃЉЃК
ГЃКШ | ВЛГЃКШ | КЯМЦ | |
ЗЪХж | 2 | ||
ВЛЗЪХж | 18 | ||
КЯМЦ | 30 |
вбжЊдкШЋВП30ШЫжаЫцЛњГщШЁ1ШЫЃЌГщЕНЗЪХжЕФбЇЩњЕФИХТЪЮЊ ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧыНЋЩЯУцЕФСаСЊБэВЙГфЭъећЃЛ
ЃЈ2ЃЉЪЧЗёга99.5%ЕФАбЮеШЯЮЊЗЪХжгыГЃКШЬМЫсвћСЯгаЙиЃПЫЕУїФуЕФРэгЩЃЛ
ЃЈ3ЃЉЯжДгГЃКШЬМЫсвћСЯЧвЗЪХжЕФбЇЩњжаЃЈ2УћХЎЩњЃЉЃЌГщШЁ2ШЫВЮМгЕчЪгНкФПЃЌдђе§КУГщЕНвЛФавЛХЎЕФИХТЪЪЧЖрЩй
PЃЈK2ЁнkЃЉ | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ЃЈВЮПМЙЋЪНЃКK2= ![]() ЃЌЦфжаn=a+b+c+dЃЉ
ЃЌЦфжаn=a+b+c+dЃЉ