Question

【题目】已知函数.

（1）若函数的图象在点处的切线方程为，求实数a，b的值；

（2）若，求的单调减区间；

（3）对一切实数，求的极小值函数，并求出的最大值.

Answer 1

【答案】（1）；（2）；（3），最大值为.

【解析】

（1）先求函数的导函数，再结合切线方程求解即可；

（2）分别讨论当时，时，求解的解集即可；

（3）解含参二次不等式，从而求出函数的单调性及极值，再求最值即可得解.

解：（1）由函数，

则

又，则，

则，

则，即；

（2）当时，由（1）得，

令，解得：，

即函数的减区间为；

当时，由（1）得，

令，解得：或，

即函数的减区间为和；

故当时，函数的减区间为；

当时，函数的减区间为和；

（3）当时，，

令，解得： ，令，解得：或，

即函数的增区间为和，减区间为，

即的极小值为，

则，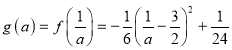

故当，即时，取最大值.