题目内容
如图,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥
平面ABCD, SA=AB=BC=2,AD=1.
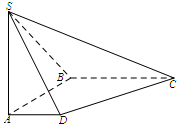
(Ⅰ)求SC与平面ASD所成的角余弦;
(Ⅱ)求平面SAB和平面SCD所成角的余弦.
平面ABCD, SA=AB=BC=2,AD=1.

(Ⅰ)求SC与平面ASD所成的角余弦;
(Ⅱ)求平面SAB和平面SCD所成角的余弦.
(Ⅰ)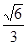 (Ⅱ)
(Ⅱ)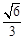
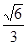 (Ⅱ)
(Ⅱ)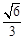
本试题主要是考查了线面角的大小的求解和二面角平面角的大小的求解的综合运用。
(1)因为利用空间直角坐标系,建立后表示点的坐标得到向量的坐标,从而利用平面的法向量和直线的方向向量来表示线面角的求解。
(2)同上结合平面的法向量来表示二面角的平面角的大小,从而得到向量的夹角相等或者互补。
解:(Ⅰ)如图建系,
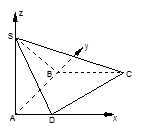
S(0,0,2), C(2,2,0), D(1,0,0),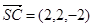
 ,故平面ASD的一个法向量为
,故平面ASD的一个法向量为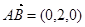 ……………3分
……………3分
设SC与平面ASD所成的角为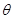 则
则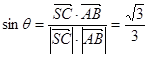
故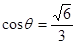 ,即SC与平面ASD所成的角余弦为
,即SC与平面ASD所成的角余弦为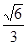 …………………6分
…………………6分
(Ⅱ)平面SAB的一个法向量为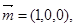
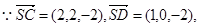 设平面SCD的一个法向量为
设平面SCD的一个法向量为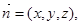
由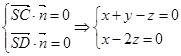 令z=1可得平面SCD的一个法向量为
令z=1可得平面SCD的一个法向量为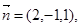
显然,平面SAB和平面SCD所成角为锐角,不妨设为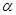 则
则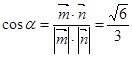
即平面SAB和平面SCD所成角的余弦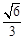 ………………12分
………………12分
(1)因为利用空间直角坐标系,建立后表示点的坐标得到向量的坐标,从而利用平面的法向量和直线的方向向量来表示线面角的求解。
(2)同上结合平面的法向量来表示二面角的平面角的大小,从而得到向量的夹角相等或者互补。
解:(Ⅰ)如图建系,

S(0,0,2), C(2,2,0), D(1,0,0),
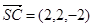
 ,故平面ASD的一个法向量为
,故平面ASD的一个法向量为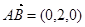 ……………3分
……………3分设SC与平面ASD所成的角为
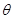 则
则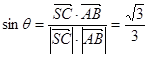
故
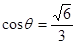 ,即SC与平面ASD所成的角余弦为
,即SC与平面ASD所成的角余弦为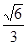 …………………6分
…………………6分(Ⅱ)平面SAB的一个法向量为
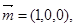
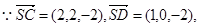 设平面SCD的一个法向量为
设平面SCD的一个法向量为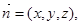
由
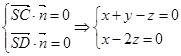 令z=1可得平面SCD的一个法向量为
令z=1可得平面SCD的一个法向量为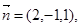
显然,平面SAB和平面SCD所成角为锐角,不妨设为
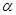 则
则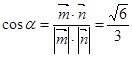
即平面SAB和平面SCD所成角的余弦
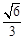 ………………12分
………………12分
练习册系列答案
相关题目

 中,若
中,若 ,则
,则 与
与 所成角为( )
所成角为( )



 中,
中, 分别是
分别是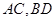 的中点,若
的中点,若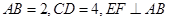 ,则
,则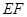 与
与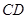 所成的角的度数为( )
所成的角的度数为( )



 中,
中, 分别是棱
分别是棱 的中点,则直线
的中点,则直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 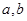 所成的角为
所成的角为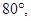 过空间一点O与
过空间一点O与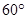 的直线有___________条
的直线有___________条 棱BB1、AD的中点,则直线EF和平面
棱BB1、AD的中点,则直线EF和平面 所成的角的正弦值是( )
所成的角的正弦值是( )




 的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是
的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是


