题目内容
已知在四面体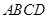 中,
中,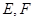 分别是
分别是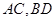 的中点,若
的中点,若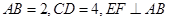 ,则
,则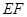 与
与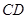 所成的角的度数为( )
所成的角的度数为( )
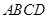 中,
中,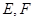 分别是
分别是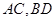 的中点,若
的中点,若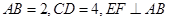 ,则
,则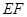 与
与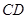 所成的角的度数为( )
所成的角的度数为( )A. | B. | C. | D. |
D
取BC的中点M,连接FM,EM,则EM//AB,FM//CD,所以 就是异面直线EF与CD所成的角,因为在
就是异面直线EF与CD所成的角,因为在 中,
中,
 .
.
 就是异面直线EF与CD所成的角,因为在
就是异面直线EF与CD所成的角,因为在 中,
中, .
.
练习册系列答案
相关题目
题目内容
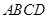 中,
中,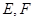 分别是
分别是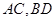 的中点,若
的中点,若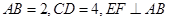 ,则
,则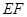 与
与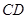 所成的角的度数为( )
所成的角的度数为( )A. | B. | C. | D. |
 就是异面直线EF与CD所成的角,因为在
就是异面直线EF与CD所成的角,因为在 中,
中, .
.