题目内容
已知底面边长为2,侧棱长为 的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是
的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是
 的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是
的正四棱锥P-ABCD内接于球O,则球面上A、B两点间的球面距离是A. | B. | C. | D. |
B
本题考查正四棱锥的概念和性质,球的性质,球面距离公式余弦定理,及空间想象能力.
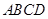 是边长为2的正方形,则
是边长为2的正方形,则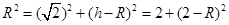 对角线为
对角线为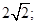 设四棱锥的高为
设四棱锥的高为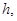 球半径为
球半径为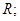 则
则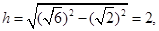 于是
于是
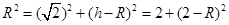 ,解得
,解得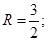 在
在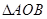 中,由余弦定理得:
中,由余弦定理得:
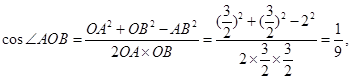 所以
所以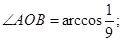 则球面上A、B两点间的球面距离是
则球面上A、B两点间的球面距离是 .故选B
.故选B
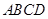 是边长为2的正方形,则
是边长为2的正方形,则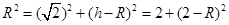 对角线为
对角线为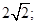 设四棱锥的高为
设四棱锥的高为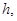 球半径为
球半径为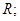 则
则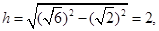 于是
于是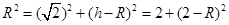 ,解得
,解得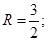 在
在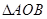 中,由余弦定理得:
中,由余弦定理得: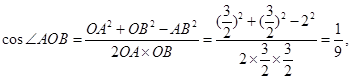 所以
所以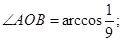 则球面上A、B两点间的球面距离是
则球面上A、B两点间的球面距离是 .故选B
.故选B
练习册系列答案
相关题目


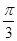
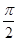
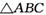 的外接圆为球O的小圆
的外接圆为球O的小圆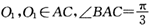 ,AB=1,PA=2.则下列结论正确的是
,AB=1,PA=2.则下列结论正确的是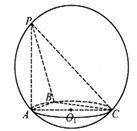

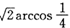
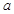 ,则相邻两个面的夹角的余弦是
,则相邻两个面的夹角的余弦是  ,其中
,其中 ,
, ,
,  ,沿
,沿 将
将 折起,使得
折起,使得 ,则二面角
,则二面角 的平面角的正弦值为 .
的平面角的正弦值为 .
 的棱长是3,点
的棱长是3,点 分别是棱
分别是棱 的中点,则异面直线MN与
的中点,则异面直线MN与 所成的角是 .
所成的角是 . 中,求对角线
中,求对角线 与对角面
与对角面 所成的角 ( )
所成的角 ( )



 ,AD=1,在DC上截取DE=1,将△ADE沿AE
,AD=1,在DC上截取DE=1,将△ADE沿AE