题目内容
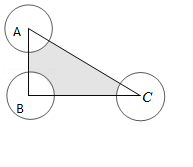
【题目】已知三个村庄A，B，C构成一个三角形，且AB=5千米，BC=12千米，AC=13千米．为了方便市民生活，现在△ABC内任取一点M建一大型生活超市，则M到A，B，C的距离都不小于2千米的概率为
A. 
B. 
C. 
D. 
【答案】C
【解析】
根据条件作出对应的图象，求出对应的面积，根据几何概型的概率公式进行计算即可．
解：在△ABC中，AB＝5，BC＝12，AC＝13，则△ABC为直角三角形，且∠B为直角。
则△ABC的面积S＝
，
若在三角形ABC内任取一点，则该点到三个定点A，B，C的距离不小于2，
则该点位于阴影部分，
则三个小扇形的圆心角转化为180°，半径为2，则对应的面积之和为S＝
，
则阴影部分的面积S＝
，
则对应的概率P＝
＝
＝
，
故选：C．
练习册系列答案
相关题目
【题目】某蛋糕店计划按天生产一种面包，每天生产量相同，生产成本每个6元，售价每个8元，未售出的面包降价处理，以每个5元的价格当天全部处理完．
（1）若该蛋糕店一天生产30个这种面包，求当天的利润
（单位：元）关于当天需求量
（单位：个，
）的函数解析式；
（2）蛋糕店记录了30天这种面包的日需求量（单位：个），整理得下表：
日需求量 | 28 | 29 | 30 | 31 | 32 | 33 |
频数 | 3 | 4 | 6 | 6 | 7 | 4 |
假设蛋糕店在这30天内每天生产30个这种面包，求这30天的日利润（单位：元）的平均数及方差．
