题目内容
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,左焦点为
,左焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于A,B两点.
交椭圆于A,B两点.
(1)求椭圆C的标准方程;
(2)在y轴上,是否存在定点E,使![]() 恒为定值?若存在,求出E点的坐标和这个定值;若不存在,说明理由.
恒为定值?若存在,求出E点的坐标和这个定值;若不存在,说明理由.
【答案】(1)![]() ;(2)存在,理由见解析.
;(2)存在,理由见解析.
【解析】
试题(1)由右焦点求得![]() 值,由离心率求得
值,由离心率求得![]() 值,进而
值,进而![]() ,从而确定椭圆方程;(2)将直线方程与椭圆方程联立,借助于根与系数的关系将
,从而确定椭圆方程;(2)将直线方程与椭圆方程联立,借助于根与系数的关系将![]() 转化为用两交点
转化为用两交点![]() 坐标来表示,进而转化为直线的斜率
坐标来表示,进而转化为直线的斜率![]() 和
和![]() 点坐标
点坐标![]() 来表示,观察关系式得到为定值时需满足的条件
来表示,观察关系式得到为定值时需满足的条件
试题解析:(1)由已知可得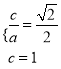 ,解得
,解得![]() ,所求的椭圆方程为
,所求的椭圆方程为![]()
(2)设点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 的方程为
的方程为![]()
由 得
得![]() ,则
,则![]()
解得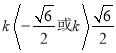
设![]() ,则
,则![]()
又![]() ,
,
![]() .
.
设存在点![]() ,则
,则![]() ,
,![]() ,
,
所以![]()
![]()
![]() ,
,
要使得![]() (
(![]() 为常数),只要
为常数),只要![]() ,
,
从而![]() ,
,
即![]()
由(1)得![]() ,
,
代入(2)解得![]() ,从而
,从而![]() ,
,
故存在定点![]() ,使
,使![]() 恒为定值
恒为定值![]() .
.

 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如下:
甲公司 | 乙公司 | |||||||||
职位 | A | B | C | D | 职位 | A | B | C | D | |
月薪/元 | 6000 | 7000 | 8000 | 9000 | 月薪/元 | 5000 | 7000 | 9000 | 11000 | |
获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | 获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | |
(1)根据以上信息,如果你是该求职者,你会选择哪一家公司?说明理由;
(2)某课外实习作业小组调查了1000名职场人士,就选择这两家公司的意愿做了统计,得到以下数据分布:
选择意愿 人员结构 | 40岁以上(含40岁)男性 | 40岁以上(含40岁)女性 | 40岁以下男性 | 40岁以下女性 |
选择甲公司 | 110 | 120 | 140 | 80 |
选择乙公司 | 150 | 90 | 200 | 110 |
若分析选择意愿与年龄这两个分类变量,计算得到的K2的观测值为k1=5.5513,测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少?并用统计学知识分析,选择意愿与年龄变量和性别变量哪一个关联性更大?
附:![]()
| 0.050 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
【题目】为了检验设备M与设备N的生产效率,研究人员作出统计,得到如下表所示的结果,则
设备M | 设备N | |
生产出的合格产品 | 48 | 43 |
生产出的不合格产品 | 2 | 7 |
附:
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式:![]() ,其中
,其中![]() .
.
A. 有90%的把握认为生产的产品质量与设备的选择有关
B. 没有90%的把握认为生产的产品质量与设备的选择有关
C. 可以在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择有关
D. 不能在犯错误的概率不超过0.1的前提下认为生产的产品质量与设备的选择有关