题目内容
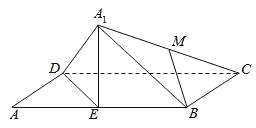
【题目】在平行四边形![]() 中,过点
中,过点![]() 的直线与线段
的直线与线段![]() 分别相交于点
分别相交于点![]() ,若
,若![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)定义函数![]() ,点列
,点列![]() 在函数
在函数![]() 的图像上,且数列
的图像上,且数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列,
为公比的等比数列,![]() 为原点,令
为原点,令![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
(3)设函数![]() 为
为![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() 函数
函数![]() 的图像关于直线
的图像关于直线![]() 对称,当方程
对称,当方程![]() 在
在![]() 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)
;(3)![]()
【解析】
(1)根据平行四边形性质得到比例关系得到答案.
(2)先计算![]() ,
,![]() 得到
得到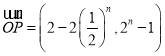 ,利用向量垂直计算得到答案.
,利用向量垂直计算得到答案.
(3)先判断![]() 周期为
周期为![]() ,得到
,得到![]() 的函数表达式,画出函数图像,根据图像计算得到答案.
的函数表达式,画出函数图像,根据图像计算得到答案.
(1)利用平行四边形性质得到![]() ,因为
,因为![]()
故![]()
(2)![]() ,
,![]()
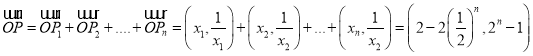
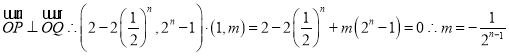
故存在![]() 使
使![]()
(3)![]() 的图像关于直线
的图像关于直线![]() 对称,函数
对称,函数![]() 为
为![]() 上的偶函数
上的偶函数
即![]() ,
,![]() 周期为
周期为![]()
故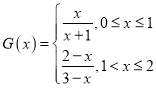
![]() 时,
时,![]()
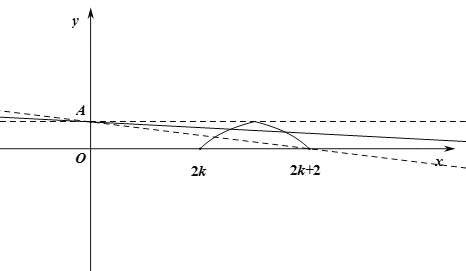
![]() 过定点
过定点![]() 如图所示,画出函数图像:
如图所示,画出函数图像:
故![]()

练习册系列答案
相关题目