题目内容
已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别为等比数列{bn}的第2项、第3项、第4项.
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}对n∈N*,均有 +
+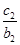 +…+
+…+ =an+1成立,求c1+c2+c3+…+c2014的值.
=an+1成立,求c1+c2+c3+…+c2014的值.
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}对n∈N*,均有
 +
+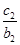 +…+
+…+ =an+1成立,求c1+c2+c3+…+c2014的值.
=an+1成立,求c1+c2+c3+…+c2014的值.(1)an=2n-1 bn=3n-1
(2)32014
(2)32014
解:(1)∵a2=1+d,a5=1+4d,a14=1+13d,
∴(1+4d)2=(1+d)(1+13d),解得d=2(∵d>0).
则an=1+(n-1)×2=2n-1.
又b2=a2=3,b3=a5=9,
∴等比数列{bn}的公比q=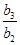 =
=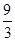 =3.
=3.
∴bn=b2qn-2=3×3n-2=3n-1.
(2)由 +
+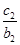 +…+
+…+ =an+1得
=an+1得
当n≥2时, +
+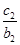 +…+
+…+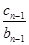 =an,
=an,
两式相减,得 =an+1-an=2,
=an+1-an=2,
∴cn=2bn=2×3n-1(n≥2).
而当n=1时, =a2,∴c1=3.
=a2,∴c1=3.
∴cn=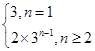
∴c1+c2+c3+…+c2014
=3+2×31+2×32+…+2×32013
=3+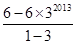
=3-3+32014
=32014.
∴(1+4d)2=(1+d)(1+13d),解得d=2(∵d>0).
则an=1+(n-1)×2=2n-1.
又b2=a2=3,b3=a5=9,
∴等比数列{bn}的公比q=
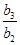 =
=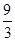 =3.
=3.∴bn=b2qn-2=3×3n-2=3n-1.
(2)由
 +
+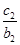 +…+
+…+ =an+1得
=an+1得当n≥2时,
 +
+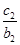 +…+
+…+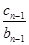 =an,
=an,两式相减,得
 =an+1-an=2,
=an+1-an=2,∴cn=2bn=2×3n-1(n≥2).
而当n=1时,
 =a2,∴c1=3.
=a2,∴c1=3.∴cn=
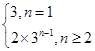
∴c1+c2+c3+…+c2014
=3+2×31+2×32+…+2×32013
=3+
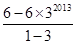
=3-3+32014
=32014.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
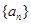 的首项
的首项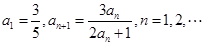 。
。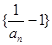 是等比数列,并求出
是等比数列,并求出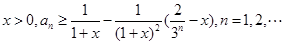 ;
;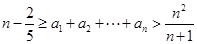 。
。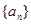 中,
中,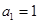 ,
,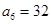 ,
, 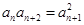 (
(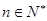 ),把数列的各项按如下方法进行分组:(
),把数列的各项按如下方法进行分组:(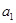 )、(
)、(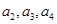 )、(
)、(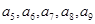 )、 ,记
)、 ,记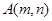 为第
为第 组的第
组的第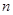 个数(从前到后),若
个数(从前到后),若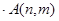 =
=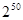 ,则
,则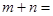 _________.
_________.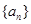 的公比为
的公比为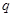 ,前
,前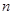 项和
项和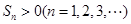 ,求
,求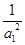 +
+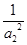 +…+
+…+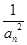 =________.
=________.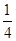 ,则Sn=a1+a2+…+an(n∈N*)的取值范围是________.
,则Sn=a1+a2+…+an(n∈N*)的取值范围是________.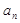 }是递增数列,
}是递增数列, 是{
是{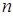 项和.若
项和.若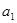 ,
,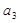 是方程
是方程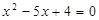 的两个根,则
的两个根,则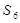 =________.
=________.