题目内容
已知数列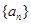 的首项
的首项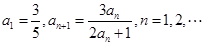 。
。
(1)求证: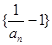 是等比数列,并求出
是等比数列,并求出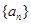 的通项公式;
的通项公式;
(2)证明:对任意的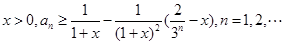 ;
;
(3)证明: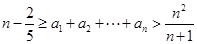 。
。
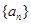 的首项
的首项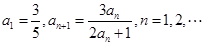 。
。(1)求证:
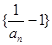 是等比数列,并求出
是等比数列,并求出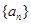 的通项公式;
的通项公式;(2)证明:对任意的
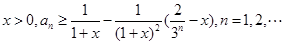 ;
;(3)证明:
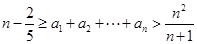 。
。(1)见解析 (2)见解析 (3)见解析
试题分析:(1)由题意
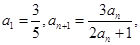 两边同时取倒数,
两边同时取倒数,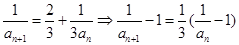 ,
,又
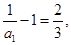 ,所以
,所以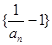 是以
是以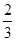 为首项,以
为首项,以 为公比的等比数列,然后由等比数列的通项公式可求出
为公比的等比数列,然后由等比数列的通项公式可求出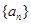 的通项公式;
的通项公式;(2)由(1)知
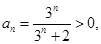 则注意到
则注意到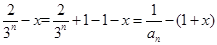 ,
,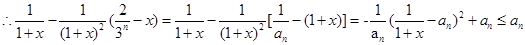 ,即可.
,即可.(3)左边不等式,由
 可得
可得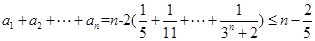 ;
;证右边不等式,由(2)知
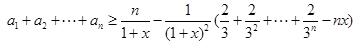 取
取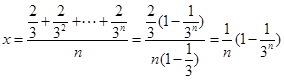 ,则
,则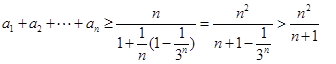
(1)
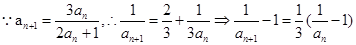 ,又
,又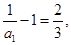 所以
所以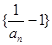 是以
是以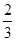 为首项,以
为首项,以 为公比的等比数列.
为公比的等比数列.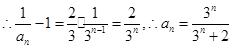
(2)由(1)知
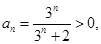
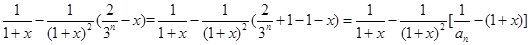
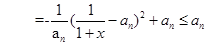
(3)先证左边不等式,由
 知
知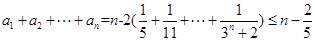 ;
;当
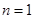 时等号成立;
时等号成立;再证右边不等式,由(2)知,对任意
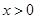 ,有
,有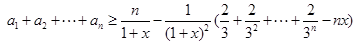 ,取
,取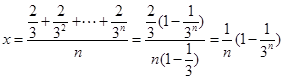 ,
,则
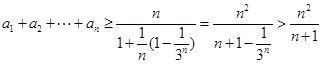

练习册系列答案
相关题目
 满足
满足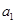 =1,
=1, .
. 是等比数列,并求
是等比数列,并求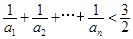 .
.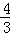 .
.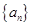 满足
满足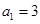 ,
,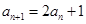 ,
,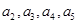 ;
; 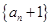 是等比数列;并求出
是等比数列;并求出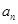 的表达式.
的表达式. +
+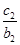 +…+
+…+ =an+1成立,求c1+c2+c3+…+c2014的值.
=an+1成立,求c1+c2+c3+…+c2014的值.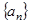 的前
的前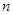 项和为
项和为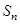 ,已知
,已知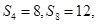 则
则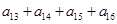 的值为 .
的值为 .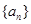 满足
满足 ,
,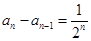 ,则
,则 = ;
= ;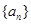 是等比数列,
是等比数列,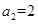 ,
,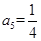 ,则公比
,则公比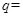 ______________.
______________.