题目内容
在利用电子邮件传播病毒的例子中,如果第一轮感染的计算机数是80台,并且从第一轮起,以后各轮的每一台计算机都可以感染下一轮的20 台计算机,到第5轮可以感染到多少台计算机?
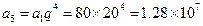
由题意可知,每一轮被感染的计算机台数构成一个首项为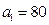 ,公比为
,公比为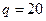 的等比数列,则第5轮被感染的计算机台数
的等比数列,则第5轮被感染的计算机台数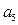 为
为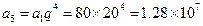 .
.
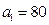 ,公比为
,公比为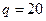 的等比数列,则第5轮被感染的计算机台数
的等比数列,则第5轮被感染的计算机台数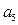 为
为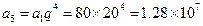 .
.
练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
题目内容
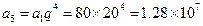
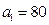 ,公比为
,公比为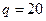 的等比数列,则第5轮被感染的计算机台数
的等比数列,则第5轮被感染的计算机台数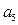 为
为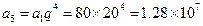 .
.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案