题目内容
已知数列an的前n项和公式为Sn=n2-23n-2(n∈N*).
(1)写出该数列的第3项;
(2)判断74是否在该数列中;
(3)确定Sn何时取最小值,最小值是多少?
(1)写出该数列的第3项;
(2)判断74是否在该数列中;
(3)确定Sn何时取最小值,最小值是多少?
(1) -18
(2) 74在该数列中.
(3)Sn=(n-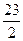 )2-
)2-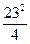 -2,
-2,
∴当n=11或n=12时,(Sn)min=-134.
(2) 74在该数列中.
(3)Sn=(n-
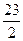 )2-
)2-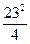 -2,
-2,∴当n=11或n=12时,(Sn)min=-134.
(1)a3=S3-S2=-18.
(2)n=1时,a1=S1=-24,
n≥2时,an=Sn-Sn-1=2n-24,
即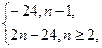
由题设得2n-24=74(n≥2),得n=49.
∴74在该数列中.
(3)Sn=(n-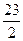 )2-
)2-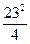 -2,
-2,
∴当n=11或n=12时,(Sn)min=-134.
(2)n=1时,a1=S1=-24,
n≥2时,an=Sn-Sn-1=2n-24,
即
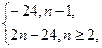
由题设得2n-24=74(n≥2),得n=49.
∴74在该数列中.
(3)Sn=(n-
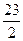 )2-
)2-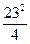 -2,
-2,∴当n=11或n=12时,(Sn)min=-134.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 ,
, ,…,
,…,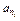 ,…是等比数列,求数列{nt}的通项公式.
,…是等比数列,求数列{nt}的通项公式.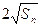 =an+1.
=an+1.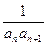 ,求数列{bn}的前n项和Bn.
,求数列{bn}的前n项和Bn.