题目内容
已知函数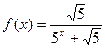 ,
,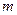 为正整数.
为正整数.
(Ⅰ)求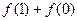 和
和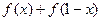 的值;
的值;
(Ⅱ)若数列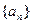 的通项公式为
的通项公式为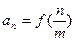 (
(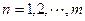 ),求数列
),求数列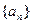 的前
的前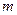 项和
项和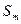 ;
;
(Ⅲ)设数列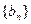 满足:
满足: ,
,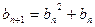 ,设
,设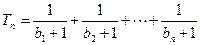 ,若(Ⅱ)中的
,若(Ⅱ)中的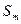 满足对任意不小于3的正整数n,
满足对任意不小于3的正整数n,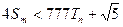 恒成立,试求m的最大值.
恒成立,试求m的最大值.
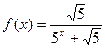 ,
,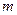 为正整数.
为正整数.(Ⅰ)求
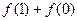 和
和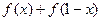 的值;
的值;(Ⅱ)若数列
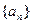 的通项公式为
的通项公式为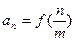 (
(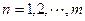 ),求数列
),求数列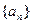 的前
的前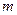 项和
项和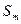 ;
;(Ⅲ)设数列
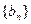 满足:
满足: ,
,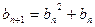 ,设
,设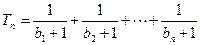 ,若(Ⅱ)中的
,若(Ⅱ)中的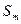 满足对任意不小于3的正整数n,
满足对任意不小于3的正整数n,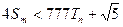 恒成立,试求m的最大值.
恒成立,试求m的最大值.(1)1,(2)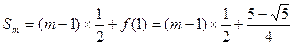 (3)650
(3)650
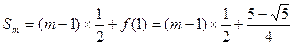 (3)650
(3)650解:(Ⅰ)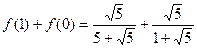 =1;
=1;
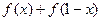 =
= =
=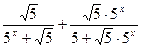 =1;………………4分
=1;………………4分
(Ⅱ)由(Ⅰ)得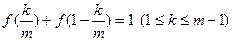 ,
,
即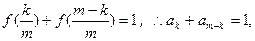
由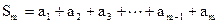 , ……………①
, ……………①
得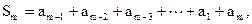 …………②
…………②
由①+②, 得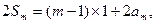 ∴
∴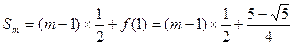 ,…10分
,…10分
(Ⅲ) ∵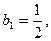
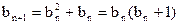 ,∴对任意的
,∴对任意的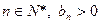 .
.
∴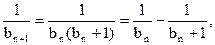 即
即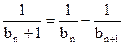 .
.
∴ .
.
∵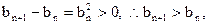 ∴数列
∴数列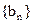 是单调递增数列.
是单调递增数列.
∴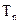 关于n递增. 当
关于n递增. 当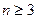 , 且
, 且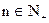 时,
时, 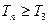 .
.
∵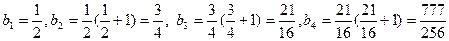
∴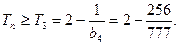 ∴
∴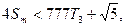 ∴
∴ .而
.而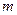 为正整数,
为正整数,
∴ 的最大值为650. ………………………14分
的最大值为650. ………………………14分
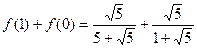 =1;
=1;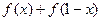 =
= =
=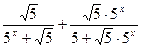 =1;………………4分
=1;………………4分(Ⅱ)由(Ⅰ)得
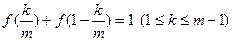 ,
,即
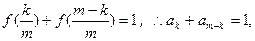
由
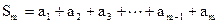 , ……………①
, ……………①得
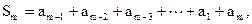 …………②
…………②由①+②, 得
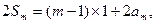 ∴
∴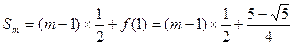 ,…10分
,…10分(Ⅲ) ∵
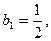
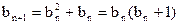 ,∴对任意的
,∴对任意的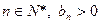 .
. ∴
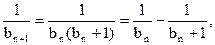 即
即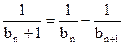 .
.∴
 .
.∵
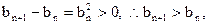 ∴数列
∴数列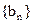 是单调递增数列.
是单调递增数列.∴
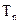 关于n递增. 当
关于n递增. 当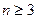 , 且
, 且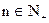 时,
时, 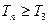 .
.∵
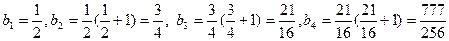
∴
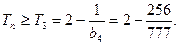 ∴
∴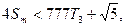 ∴
∴ .而
.而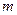 为正整数,
为正整数,∴
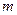 的最大值为650. ………………………14分
的最大值为650. ………………………14分
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
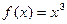 ,等差数列
,等差数列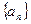 中
中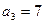 ,
,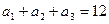 ,记
,记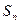 =
=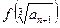 ,令
,令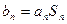 ,数列
,数列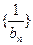 的前n项和为
的前n项和为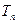 .
.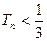 ;
;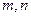 ,且
,且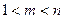 ,使得
,使得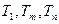 成等比数列?若存在,求出
成等比数列?若存在,求出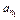 ,
,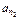 ,…,
,…,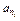 ,…是等比数列,求数列{nt}的通项公式.
,…是等比数列,求数列{nt}的通项公式.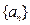 的前
的前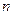 项和为
项和为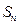 ,若对所有正整数
,若对所有正整数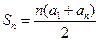 .
.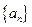 的公差
的公差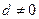 ,记
,记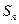 为数列
为数列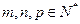 ,且
,且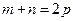 ,则
,则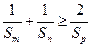 ;
;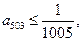 则
则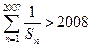 。
。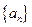 中,已知
中,已知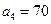 ,
,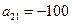 .
.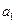 与公差
与公差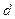 ,并写出通项公式;
,并写出通项公式;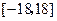 ?
?