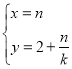题目内容
【题目】在直角坐标平面中,△ABC的两个顶点A、B的坐标分别为A(﹣1,0),B (1,0),平面内两点G、M同时满足下列条件:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ∥
∥![]() ,则△ABC的顶点C的轨迹方程为_____.
,则△ABC的顶点C的轨迹方程为_____.
【答案】x2![]() 1(y≠0)
1(y≠0)
【解析】
由题目给出的条件,分别得到G为三角形ABC的重心,M为三角形ABC的外心,设出G点坐标,由![]() ,可知M和G具有相同的纵坐标,由重心坐标公式得到C点的坐标,然后由M到A和C的距离相等列式可得G的轨迹方程,利用代入法转化为C的轨迹方程.
,可知M和G具有相同的纵坐标,由重心坐标公式得到C点的坐标,然后由M到A和C的距离相等列式可得G的轨迹方程,利用代入法转化为C的轨迹方程.
解:由![]() 得,G为重心,
得,G为重心,
由![]() 得,M为外心.
得,M为外心.
所以M点在y轴上(M到AB两点距离相等).
又![]() ,则
,则![]() .
.
设M为(0,y),G为(x,y)(y≠0),由重心坐标公式得C为(3x,3y).
再由MA=MC,得![]() 整理得:9x2+3y2=1①.
整理得:9x2+3y2=1①.
再设c(x',y'),由3x=x',3y=y'得x![]() ,y
,y![]() .
.
代入①得:(x′)2![]() 1.
1.
所以△ABC的顶点C的轨迹方程为![]() ,
,![]() .
.
故答案为: ![]() ,
,![]() .
.

练习册系列答案
相关题目