题目内容
(本小题满分12分)
己知圆C: (x – 2 )2 + y 2 =" 9," 直线l:x + y = 0.
(1) 求与圆C相切, 且与直线l平行的直线m的方程;
(2) 若直线n与圆C有公共点,且与直线l垂直,求直线n在y轴上的截距b的取值范围;
(1) x + y – 2 +3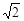 ="0," 或x + y – 2 –3
="0," 或x + y – 2 –3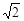 ="0." (2) – 2–3
="0." (2) – 2–3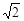 £ b £ – 2+3
£ b £ – 2+3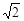
解析试题分析:(1) ∵直线m∥直线x + y = 0,
∴设m: x + y + c = 0,∵直线m与圆C相切,∴ 3 = 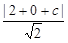 ,
,
解得 c =" –" 2 ±3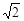
得直线m的方程为:x + y – 2 +3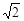 ="0," 或x + y – 2 –3
="0," 或x + y – 2 –3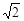 ="0."
="0."
(2) 由条件设直线n的方程为:y = x +b ,
代入圆C方程整理得:2x2 +2 (b – 2)x + b2 – 5 = 0,
∵直线l与圆C有公共点,
∴ △ =" 4(b" – 2)2 – 8(b2 – 5 ) =" –" 4b2 – 16b +56 ≥ 0,即:b2 + 4b –14 £ 0
解得:– 2–3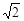 £ b £ – 2+3
£ b £ – 2+3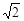
考点:本试题考查了两直线的位置关系。
点评:运用两直线的平行的关系来设出所求的直线方程,并代点来求解方程。同时要理解截距的概念,表示的为数字,不是距离,是一个可正可负的数字。结合直线与圆的位置关系得到取值范围,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,已知圆
中,已知圆 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 .
. ,B(
,B( ), C(0,6)的圆的方程,并指出这个圆的半径和圆心坐标.
), C(0,6)的圆的方程,并指出这个圆的半径和圆心坐标. 截直线
截直线 的弦长为
的弦长为 ;
; 的值;
的值; 的圆的切线所在的直线方程.
的圆的切线所在的直线方程. 经过点
经过点 ,且和圆
,且和圆 相交,截得的弦长为4
相交,截得的弦长为4 ,求直线
,求直线 ,圆心在直线
,圆心在直线 上,且被直线
上,且被直线 截得的弦长为
截得的弦长为 ,求圆C的方程
,求圆C的方程 ,直线
,直线 以及
以及 上一点
上一点 .
.
 上且与直线
上且与直线 的圆⊙M的方程.
的圆⊙M的方程. 分别与直线
分别与直线 、圆⊙依次相交于A、B、C三点,
、圆⊙依次相交于A、B、C三点, .
.  上,且经过圆
上,且经过圆 与圆
与圆 的交点的圆方程.
的交点的圆方程.
 上的动点到焦点距离的最小值为
上的动点到焦点距离的最小值为 。以原点为圆心、椭圆的短半轴长为半径的圆与直线
。以原点为圆心、椭圆的短半轴长为半径的圆与直线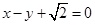 相切.
相切. 的方程;
的方程; (2,0)的直线与椭圆
(2,0)的直线与椭圆 两点,
两点, 为椭圆上一点, 且满足
为椭圆上一点, 且满足 (
( 为坐标原点)。当
为坐标原点)。当 时,求实数
时,求实数 的值.
的值.