题目内容
已知圆C的半径为 ,圆心在直线
,圆心在直线 上,且被直线
上,且被直线 截得的弦长为
截得的弦长为 ,求圆C的方程
,求圆C的方程
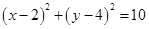 或
或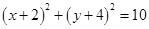 .
.
解析试题分析:因为所求圆的圆心C在直线 上,所以设圆心为
上,所以设圆心为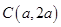 ,
,
所以可设圆的方程为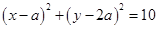 ,
,
因为圆被直线 截得的弦长为
截得的弦长为 ,则圆心
,则圆心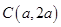 到直线
到直线 的距离
的距离 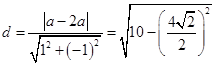 ,即
,即 ,解得
,解得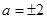 .
.
所以圆的方程为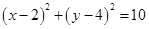 或
或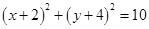 .
.
考点:圆的方程;直线与圆的位置关系;点到直线的距离公式。
点评:(1)要求圆的方程,只需确定圆心和半径。(2)当直线与圆相交时,通常用到弦心距、半径、弦长的一半构成的直角三角形来求解。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 轴正半轴上,直线
轴正半轴上,直线 与圆C相切
与圆C相切 的直线
的直线 与圆C交于不同的两点
与圆C交于不同的两点 且为
且为 时,求:
时,求: 的面积.
的面积. (t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位。且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位。且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
 的最小值.
的最小值. :
:
 为参数),圆
为参数),圆 (极轴与
(极轴与 轴的非负半轴重合,且单位长度相同)。
轴的非负半轴重合,且单位长度相同)。 到直线
到直线 ,求
,求 的值。
的值。 上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
 与两平行直线
与两平行直线 都相切,且圆心
都相切,且圆心 在直线
在直线 上,
上, 与
与 两点,
两点, 为坐标原点且满足
为坐标原点且满足 ,求直线
,求直线 :
: 的焦点为圆
的焦点为圆 的圆心,直线
的圆心,直线 与
与 交于不同的两点
交于不同的两点 .
. 。
。