题目内容
【题目】已知三棱锥![]() 中,
中,![]() 面
面![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,则该三棱锥的外接球的表面积为__________.
,则该三棱锥的外接球的表面积为__________.
【答案】![]()
【解析】
根据题意,证出BC⊥平面SAC,可得BC⊥SC,得Rt△BSC的中线OC![]() SB,同理得到OA
SB,同理得到OA![]() SB,因此O是三棱锥S﹣ABC的外接球心.利用勾股定理结合题中数据算出SC,得外接球半径R=
SB,因此O是三棱锥S﹣ABC的外接球心.利用勾股定理结合题中数据算出SC,得外接球半径R=![]() ,从而得到所求外接球的表面积.
,从而得到所求外接球的表面积.
取SB的中点O,连结OA、OC
∵SA⊥平面ABC,AB平面ABC,
∴SA⊥AB,可得Rt△ASB中,中线OA![]() SB
SB
由![]() ,
,![]() ,
,![]() ,可知:AC⊥BC,
,可知:AC⊥BC,
又∵SA⊥BC, SA、AB是平面SAB内的相交直线
∴BC⊥平面SAC,可得BC⊥SC
因此Rt△BSC中,中线OC![]() SB
SB
∴O是三棱锥S﹣ABC的外接球心,
∵Rt△SBA中,AB![]() ,SA=6
,SA=6
∴SB=2,可得外接球半径R![]() SB=
SB=![]()
因此,外接球的体积S![]() Πr2
Πr2![]() π
π
故答案为:![]() π.
π.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过
向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过![]() 转赠给好友.某用户共获得了
转赠给好友.某用户共获得了![]() 张骑行券,其中只有
张骑行券,其中只有![]() 张是一元券.现该用户从这
张是一元券.现该用户从这![]() 张骑行券中随机选取
张骑行券中随机选取![]() 张转赠给好友,求选取的
张转赠给好友,求选取的![]() 张中至少有
张中至少有![]() 张是一元券的概率.
张是一元券的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
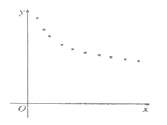
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作价格
哪一个更适宜作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() (
(![]() ),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为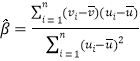 ,
,![]() .
.