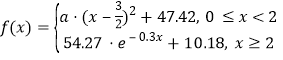ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥÷÷–¬≤ζΤΖΆΕΖ≈ –≥Γ“ΜΕΈ ±ΦδΚσΘ§Ψ≠ΙΐΒς―–ΜώΒΟΝΥ ±Φδ![]() Θ®Χλ ΐΘ©”κœζ έΒΞΦέ
Θ®Χλ ΐΘ©”κœζ έΒΞΦέ![]() Θ®‘ΣΘ©ΒΡ“ΜΉι ΐΨίΘ§«“ΉωΝΥ“ΜΕ®ΒΡ ΐΨί¥ΠάμΘ®»γ±μΘ©Θ§≤ΔΉς≥ωΝΥ…ΔΒψΆΦΘ®»γΆΦΘ©
Θ®‘ΣΘ©ΒΡ“ΜΉι ΐΨίΘ§«“ΉωΝΥ“ΜΕ®ΒΡ ΐΨί¥ΠάμΘ®»γ±μΘ©Θ§≤ΔΉς≥ωΝΥ…ΔΒψΆΦΘ®»γΆΦΘ©
|
|
|
|
|
|
|
|
|
|
|
|
|
|
±μ÷–![]() Θ§
Θ§![]() .
.
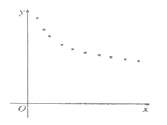
Θ®1Θ©ΗυΨί…ΔΒψΆΦ≈–ΕœΘ§![]() ”κ
”κ![]() ΡΡ“ΜΗωΗϋ “ΥΉςΦέΗώ
ΡΡ“ΜΗωΗϋ “ΥΉςΦέΗώ![]() ΙΊ”Ύ ±Φδ
ΙΊ”Ύ ±Φδ![]() ΒΡΜΊΙιΖΫ≥Χάύ–ΆΘΩΘ®≤Μ±ΊΥΒΟςάμ”…Θ©
ΒΡΜΊΙιΖΫ≥Χάύ–ΆΘΩΘ®≤Μ±ΊΥΒΟςάμ”…Θ©
Θ®2Θ©ΗυΨί≈–ΕœΫαΙϊΚΆ±μ÷– ΐΨίΘ§Ϋ®ΝΔ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΜΊΙιΖΫ≥ΧΘΜ
ΒΡΜΊΙιΖΫ≥ΧΘΜ
Θ®3Θ©»τΗΟ≤ζΤΖΒΡ»’œζ έΝΩ![]() Θ®ΦΰΘ©”κ ±Φδ
Θ®ΦΰΘ©”κ ±Φδ![]() ΒΡΚ· ΐΙΊœΒΈΣ
ΒΡΚ· ΐΙΊœΒΈΣ![]() Θ®
Θ®![]() Θ©Θ§«σΗΟ≤ζΤΖΆΕΖ≈ –≥ΓΒΎΦΗΧλΒΡœζ έΕνΉνΗΏΘΩΉνΗΏΈΣΕύ…Ό‘ΣΘΩΘ®ΫαΙϊ±ΘΝτ’ϊ ΐΘ©
Θ©Θ§«σΗΟ≤ζΤΖΆΕΖ≈ –≥ΓΒΎΦΗΧλΒΡœζ έΕνΉνΗΏΘΩΉνΗΏΈΣΕύ…Ό‘ΣΘΩΘ®ΫαΙϊ±ΘΝτ’ϊ ΐΘ©
ΗΫΘΚΕ‘”Ύ“ΜΉι ΐΨί![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§ΤδΜΊΙι÷±œΏ
Θ§ΤδΜΊΙι÷±œΏ![]() ΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΖ÷±πΈΣ
ΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΖ÷±πΈΣ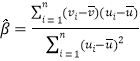 Θ§
Θ§![]() .
.
ΓΨ¥πΑΗΓΩ(1)ΦϊΫβΈω;(2)![]() ;(3)ΗΟ≤ζΤΖΆΕΖ≈ –≥ΓΒΎ
;(3)ΗΟ≤ζΤΖΆΕΖ≈ –≥ΓΒΎ![]() ΧλΒΡœζ έΕνΉνΗΏΘ§ΉνΗΏ‘ΦΈΣ
ΧλΒΡœζ έΕνΉνΗΏΘ§ΉνΗΏ‘ΦΈΣ![]() ‘Σ.
‘Σ.
ΓΨΫβΈωΓΩΖ÷ΈωΘΚΘ®1Θ©Χβ…η÷–Ηχ≥ωΒΡ…ΔΒψΆΦάύΥΤ”ΎΖ¥±»άΐΚ· ΐΘ§Ψί¥ΥΩ…“‘―Γ≥ωΜΊΙιΖΫ≥ΧΒΡάύ–Ά.
Θ®2Θ©ΗυΨίΗχ≥ωΒΡΙΪ ΫΦΤΥψΜΊΙιΖΫ≥ΧΦ¥Ω….
Θ®3Θ©ΗυΨίΜΊΙιΖΫ≥ΧΚΆ![]() ΒΟΒΫ»’œζ έΕνΒΡΚ· ΐΘ§≈δΖΫΚσΩ…«σΚ· ΐΒΡΉν¥σ÷Β.
ΒΟΒΫ»’œζ έΕνΒΡΚ· ΐΘ§≈δΖΫΚσΩ…«σΚ· ΐΒΡΉν¥σ÷Β.
œξΫβΘΚΘ®1Θ©”……ΔΒψΆΦΩ…“‘≈–Εœ![]() ΚœΉςΉςΦέΗώ
ΚœΉςΉςΦέΗώ![]() ΙΊ”Ύ ±Φδ
ΙΊ”Ύ ±Φδ![]() ΒΡΜΊΙιΖΫ≥Χάύ–ΆΘΜ
ΒΡΜΊΙιΖΫ≥Χάύ–ΆΘΜ
Θ®2Θ©Νν![]() Θ§œ»Ϋ®ΝΔ
Θ§œ»Ϋ®ΝΔ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ§”…”Ύ
ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ§”…”Ύ![]() Θ§
Θ§
Γύ![]() Θ§Γύ
Θ§Γύ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΖΫ≥ΧΈΣ
ΒΡœΏ–‘ΖΫ≥ΧΈΣ![]() Θ§
Θ§
Γύ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΖΫ≥ΧΈΣ
ΒΡœΏ–‘ΖΫ≥ΧΈΣ![]()
Θ®3Θ©…η»’œζ έΕνΈΣ![]() Θ§‘ρ
Θ§‘ρ![]()
![]()
![]() Θ§
Θ§
Γύ![]() ±Θ§
±Θ§![]() Θ®‘ΣΘ©
Θ®‘ΣΘ©
Φ¥ΗΟ≤ζΤΖΆΕΖ≈ –≥ΓΒΎ![]() ΧλΒΡœζ έΕνΉνΗΏΘ§ΉνΗΏ‘ΦΈΣ
ΧλΒΡœζ έΕνΉνΗΏΘ§ΉνΗΏ‘ΦΈΣ![]() ‘Σ.
‘Σ.

ΓΨΧβΡΩΓΩ“―÷ΣΝΔΖΫΚΆΙΪ ΫΘΚ![]()
![]() «σΚ· ΐ
«σΚ· ΐ![]() ΒΡ÷Β”ρΘΜ
ΒΡ÷Β”ρΘΜ
![]() «σΚ· ΐ
«σΚ· ΐ![]() Θ§
Θ§![]() ΒΡ÷Β”ρΘΜ
ΒΡ÷Β”ρΘΜ
![]() »τ»Έ“β Β ΐxΘ§≤ΜΒ» Ϋ
»τ»Έ“β Β ΐxΘ§≤ΜΒ» Ϋ![]() Κψ≥…ΝΔΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
Κψ≥…ΝΔΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫ»Υ‘ΎœύΆ§ΧθΦΰœ¬Ης¥ρΑ–10¥Έ,ΟΩ¥Έ¥ρΑ–ΥυΒΟΒΡΜΖ ΐ»γΆΦΥυ Ψ.
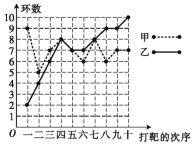
Χν–¥œ¬±μΘ§«κ¥”œ¬Ν–Ϋ«Ε»Ε‘’β¥ΈΫαΙϊΫχ––Ζ÷Έω.
Οϋ÷–9ΜΖΦΑ“‘…œΒΡ¥Έ ΐ | ΤΫΨυ ΐ | ÷–ΈΜ ΐ | ΖΫ≤ν | |
ΦΉ | ||||
““ |
(1)Οϋ÷–9ΜΖΦΑ“‘…œΒΡ¥Έ ΐ(Ζ÷ΈωΥ≠ΒΡ≥…Φ®ΚΟ–©);
(2)ΤΫΨυ ΐΚΆ÷–ΈΜ ΐ(Ζ÷ΈωΥ≠ΒΡ≥…Φ®ΚΟ–©);
(3)ΖΫ≤ν(Ζ÷ΈωΥ≠ΒΡ≥…Φ®ΗϋΈ»Ε®);
(4)’έœΏΆΦ…œΝΫ»Υ…δΜςΟϋ÷–ΜΖ ΐΒΡΉΏ Τ(Ζ÷ΈωΥ≠Ηϋ”–«±ΝΠ).