题目内容
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,圆
,圆![]() :
:![]() 与
与![]() 轴的正半轴的交点是
轴的正半轴的交点是![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() .
.

(1)若直线![]() 与
与![]() 轴交于
轴交于![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的中点为
的中点为![]() ,点
,点![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() (2)-1(3)
(2)-1(3)![]()
【解析】
(1)可设点![]() ,表示出
,表示出![]() ,可求出参数
,可求出参数![]() 或6,结合题意可舍去
或6,结合题意可舍去![]() ,再由
,再由![]() 两点已知求出直线
两点已知求出直线![]() 的方程;
的方程;
(2)可设![]() ,设直线方程为
,设直线方程为![]() ,联立直线和圆的方程求出关于
,联立直线和圆的方程求出关于![]() 的一元二次方程,表示出韦达定理,再分别求出
的一元二次方程,表示出韦达定理,再分别求出![]() ,结合前式即可求解;
,结合前式即可求解;
(3)设![]() ,由
,由![]() 建立方程,化简可得
建立方程,化简可得![]() ,由(2)可得
,由(2)可得 ,联立求解得
,联立求解得![]() ,再结合圆的几何性质和点到直线距离公式及三角形面积公式即可求解;
,再结合圆的几何性质和点到直线距离公式及三角形面积公式即可求解;
(1)设![]() ,求出
,求出![]() ,
,![]() ,
,
则![]() 或6,结合直线圆的位置关系可知,
或6,结合直线圆的位置关系可知,![]() 一定满足,
一定满足,![]() ,
,![]() 此时直线
此时直线![]() 的方程为:
的方程为:![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,圆心到直线距离
,圆心到直线距离![]() (舍去);
(舍去);
(2)设直线![]() 的方程为:
的方程为:![]() ,联立
,联立
可得:![]() ,
,
设![]() ,则
,则 ,①
,①
![]() ,
,
则![]() ,②
,②
将①代入②化简可得![]() ,
,
即![]() ;
;
(3)设点![]() ,由点
,由点![]() ,
,![]() ,
,
可得![]() ,化简得
,化简得![]() ,③
,③
又 ,④
,④
④式代入③式解得![]() 或
或![]() ,由圆心到直线的距离
,由圆心到直线的距离![]() ,故
,故![]() ,此时
,此时![]() ,圆心到直线距离
,圆心到直线距离![]() ,
,
则 ,直线方程为:
,直线方程为:![]() ,
,![]() ,
,![]() 到直线的距离
到直线的距离![]() ,则
,则![]()


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】甲、乙两人在相同条件下各射击![]() 次,每次中靶环数情况如图所示:
次,每次中靶环数情况如图所示:
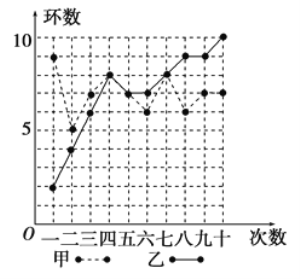
(1)请填写下表(先写出计算过程再填表):
平均数 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
(2)从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中![]() 环及
环及![]() 环以上的次数相结合看(分析谁的成绩好些);
环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).