题目内容
1．在集合{（x，y）|0≤x≤4，0≤y≤4}内任取1个元素，能使式子x+y-6≥0的概率为$\frac{1}{8}$．分析 由题意，本题符合几何概型，只要求出在集合{（x，y）|0≤x≤4，0≤y≤4}内任取1个元素对应的区域面积，以及能使式子x+y-6≥0的区域面积，利用几何概型公式可得．
解答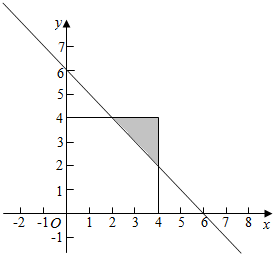 
解：在集合{（x，y）|0≤x≤4，0≤y≤4}内任取1个元素，对应的区域面积为4×4=16，
能使式子x+y-6≥0的如图中阴影部分，对应的面积为$\frac{1}{2}×2×2$=2，
由几何概型公式可得能使式子x+y-6≥0的概率为：$\frac{2}{16}=\frac{1}{8}$；
故答案为：$\frac{1}{8}$．
点评 本题考查了几何概型公式的运用，关键是由题意，明确所求为对应区域的面积比．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
11．已知实数x，y满足不等式组$\left\{\begin{array}{l}{x+y≤3}\\{x+y≥2}\\{x≥0，y≥0}\end{array}\right.$若z=x-y，则z的最大值为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
16．已知F1是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，过F1且垂直于x轴的直线与双曲线交于A、B两点，E是双曲线的右顶点，若△ABE是钝角三角形，则该双曲线的离心率的取值范围是（ ）
| A． | （1，$\sqrt{3}$） | B． | （$\sqrt{3}$，2） | C． | （2，+∞） | D． | （1，2） |
6．复数z满足z（$\overline{z}$+1）=1+i，其中i是虚数单位，则z=（ ）
| A． | 1+i或-2+i | B． | i或1+i | C． | i或-1+i | D． | -1-i或-2+i |
13．已知f（x+1）是周期为2的奇函数，当-1≤x≤0时，f（x）=-2x（x+1），则f（-$\frac{3}{2}$）的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | -$\frac{1}{4}$ | D． | -$\frac{1}{2}$ |
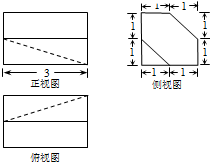
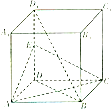如图，正方体ABCD-A1B1C1D1中，E为线段DD1的中点