题目内容
20.在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且EB=AB=2,CD=1,(1)求二面角D-AB-C的正切值
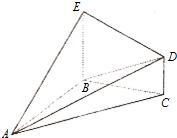
(2)求AD与平面ABE所成角的正弦值.
分析 (1)由条件证明AB⊥平面BEDC,可得∠DBC为二面角D-AB-C的平面角.解直角三角形BCD,求得tan∠DBC=CDBC 的值.
(2)取BE得中点N,则DN⊥BE.由平面和平面垂直的性质可得DN⊥平面ABE,∠DAN即为AD与平面ABE所成角.再根据sin∠DAN=DNDA,求得结果.
解答  解:(1)等腰直角三角形ABC中,∠ABC=90°,∴AB⊥BC.
解:(1)等腰直角三角形ABC中,∠ABC=90°,∴AB⊥BC.
又BE和CD都垂直于平面ABC,∴AB⊥BE,∴AB⊥平面BEDC,∴∠DBC为二面角D-AB-C的平面角.
直角三角形BCD中,由EB=AB=2,CD=1,可得tan∠DBC=CDBC=12.
(2)由于DB=DE=√5,故△DBE为等腰三角形,取BE得中点N,则DN⊥BE.
由(1)AB⊥平面BEDC,可得平面ABE⊥平面BEDC,且平面ABE和平面BEDC 的交线为BE,
故DN⊥平面ABE,∠DAN即为AD与平面ABE所成角.
sin∠DAN=DNDA=2√(2√2)2+1=23.
点评 本题主要考查直线和平面成的角的定义和求法,平面和平面垂直的性质,二面角的平面角的定义和求法,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
16.已知F1是双曲线x2a2-y2b2=1(a>0,b>0)的左焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,E是双曲线的右顶点,若△ABE是钝角三角形,则该双曲线的离心率的取值范围是( )
| A. | (1,√3) | B. | (√3,2) | C. | (2,+∞) | D. | (1,2) |
15.在同一坐标系中,将椭圆x216+y225=1变换成单位圆的伸缩变换是( )
| A. | φ:{x′=5xy′=4y | B. | φ:{x′=4xy′=5y | ||
| C. | φ:{x′=14xy′=15y | D. | φ:{x′=15xy′=14y |
10.在△ABC内部随机取一点P,则事件“△PBC”的面积不大于△ABC面积的14”的概率是( )
| A. | 716 | B. | 916 | C. | 59 | D. | 49 |
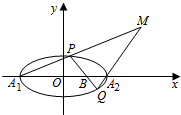 如图,已知椭圆C:
如图,已知椭圆C: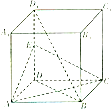 如图,正方体ABCD-A1B1C1D1中,E为线段DD1的中点
如图,正方体ABCD-A1B1C1D1中,E为线段DD1的中点