题目内容
17．若x，y∈R且满足x+3y=2，则3x+27y+1的最小值是（ ）| A． | 3$\root{3}{9}$ | B． | 1+2$\sqrt{2}$ | C． | 7 | D． | 6 |
分析 化简3x+27y+1=3x+33y+1，从而利用基本不等式确定最小值即可．
解答 解：3x+27y+1=3x+33y+1
≥2$\sqrt{{3}^{x}•{3}^{3y}}$+1
=2$\sqrt{{3}^{x+3y}}$+1
=2•3+1=7；
（当且仅当3x=33y，x+3y=2；即x=1，y=$\frac{1}{3}$时，等号成立）；
故3x+27y+1的最小值是7；
故选：C．
点评 本题考查了基本不等式的基本应用及幂运算的应用，属于中档题．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13．已知f（x+1）是周期为2的奇函数，当-1≤x≤0时，f（x）=-2x（x+1），则f（-$\frac{3}{2}$）的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | -$\frac{1}{4}$ | D． | -$\frac{1}{2}$ |
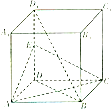如图，正方体ABCD-A1B1C1D1中，E为线段DD1的中点
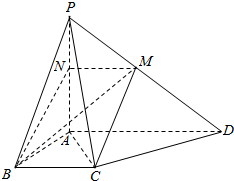如图所示，四棱锥P-ABCD的底面ABCD是直角梯形，BC∥AD，AB⊥AD，AB=BC=$\frac{1}{2}$AD，PA⊥底面ABCD，过BC的平面交PD于M，交PA与N（M与D不重合）．