题目内容
15.今年柴静的《穹顶之下》发布后,各地口罩市场受其影响生意火爆.A市虽然雾霾现象不太严重,但经抽样有25%的市民表示会购买口罩.现将频率视为概率,解决下列问题:(1)从该市市民中随机抽取3位,求至少有一位市民会购买口罩的概率;
(2)从该市市民中随机抽取4位,X表示愿意购买口罩的市民人数,求X的分布列及数学期望.
分析 (1)设“某市民还会购买口罩”为事件A,则P(A)=0.25.设X表示“该市市民中随机抽取3位中还会购买口罩的人数”.由P(X≥1)=1-P(X=0)即可得出.
(2)由题意可知:X=0,1,2,3,4.求出相应的概率,可得X的分布列及数学期望.
解答 解:(1)设“某市民还会购买口罩”为事件A,则P(A)=0.25.
设X表示“该市市民中随机抽取3位中会购买口罩的人数”.
P(X≥1)=1-P(X=0)=1-(1-0.25)3=$\frac{37}{64}$.
(2)由题意可知:X=0,1,2,3,4.
P(X=0)=(1-0.25)4=$\frac{81}{256}$,P(X=1)=${C}_{4}^{1}$×0.25×(1-0.25)3=$\frac{27}{64}$
P(X=2)=${C}_{4}^{2}$×0.252×(1-0.25)2=$\frac{54}{256}$,
P(X=3)=${C}_{4}^{3}$×0.253×(1-0.25)=$\frac{12}{256}$,
P(X=4)=0.254=$\frac{1}{256}$.
X的分布列
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{81}{256}$ | $\frac{27}{64}$ | $\frac{54}{256}$ | $\frac{12}{256}$ |
点评 本题考查了独立事件和互斥事件的概率计算公式、分类讨论的思想方法等基础知识与基本方法,考查分布列及数学期望,属于难题.

练习册系列答案
相关题目
10.在△ABC内部随机取一点P,则事件“△PBC”的面积不大于△ABC面积的$\frac{1}{4}$”的概率是( )
| A. | $\frac{7}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{9}$ |
20.已知角θ的顶点为坐标原点O,始边为x轴的非负半轴,且满足sin$\frac{θ}{2}$=$-\frac{3}{5}$,cos$\frac{θ}{2}$=$\frac{4}{5}$,设B为角θ终边上任意一点,$\overrightarrow{OA}=(0,-1)$,则|$\overrightarrow{OA}-\overrightarrow{OB}$|的取值范围是( )
| A. | [$\frac{7}{25},+∞)$ | B. | [$\frac{1}{3}$,+∞) | C. | [$\frac{4}{5}$,+∞) | D. | [1,+∞) |
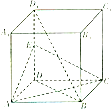 如图,正方体ABCD-A1B1C1D1中,E为线段DD1的中点
如图,正方体ABCD-A1B1C1D1中,E为线段DD1的中点 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA与N(M与D不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA与N(M与D不重合).