题目内容
10.已知{an}为等差数列,Sn为其前n项和,若a3=-6,S1=S3,则公差d=-12; Sn的最大值为24.分析 由题意列式求得首项和公差,写出等差数列的前n项和,利用配方法求得最值.
解答 解:由a3=-6,S1=S3,得
$\left\{\begin{array}{l}{{a}_{1}+2d=-6}\\{{a}_{1}=3{a}_{1}+3d}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{a}_{1}=18}\\{d=-12}\end{array}\right.$.
∴${S}_{n}=18n+\frac{n(n-1)×(-12)}{2}=-6{n}^{2}+24n$=-6(n-2)2+24.
∴当n=2时,Sn有最大值为24.
故答案为:-12,24.
点评 本题考查等差数列的通项公式,考查等差数列的前n项和,是基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
6.复数z满足z($\overline{z}$+1)=1+i,其中i是虚数单位,则z=( )
| A. | 1+i或-2+i | B. | i或1+i | C. | i或-1+i | D. | -1-i或-2+i |
20.已知角θ的顶点为坐标原点O,始边为x轴的非负半轴,且满足sin$\frac{θ}{2}$=$-\frac{3}{5}$,cos$\frac{θ}{2}$=$\frac{4}{5}$,设B为角θ终边上任意一点,$\overrightarrow{OA}=(0,-1)$,则|$\overrightarrow{OA}-\overrightarrow{OB}$|的取值范围是( )
| A. | [$\frac{7}{25},+∞)$ | B. | [$\frac{1}{3}$,+∞) | C. | [$\frac{4}{5}$,+∞) | D. | [1,+∞) |
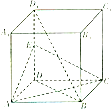 如图,正方体ABCD-A1B1C1D1中,E为线段DD1的中点
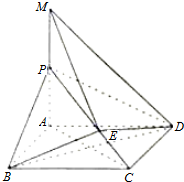
如图,正方体ABCD-A1B1C1D1中,E为线段DD1的中点 如图,四棱锥P-ABCD的底面是直角梯形,∠BAD=∠CDA=90°,侧面PAD⊥底面ABCD,AB=PD=1,PA=DC=2,AD=$\sqrt{3}$,点E是BC的中点.
如图,四棱锥P-ABCD的底面是直角梯形,∠BAD=∠CDA=90°,侧面PAD⊥底面ABCD,AB=PD=1,PA=DC=2,AD=$\sqrt{3}$,点E是BC的中点.