��Ŀ����
����Ŀ��ij����ʱ���շѣ��շѱ�Ϊ��ÿ��һ�β�����1Сʱ�շ�10Ԫ������1Сʱ�IJ���ÿСʱ�շ�8Ԫ������1Сʱ�IJ��ְ�1Сʱ���㣩�����мס��Ҷ��˲��뵫��������4Сʱ���ס��Ҷ�����ÿ��ʱ���볡�ǵȿ��ܵģ�Ϊ�����˿ͣ�ÿ���˿Ϳ��Բμ�һ�γ齱���
��1���ã�10��10����ʾ�����涼������1Сʱ�ĸ����������ס��Ҷ��˸���֮��Ϊ44Ԫ�ĸ��ʣ�
��2���齱��Ĺ����ǣ��˿�ͨ����������ʹ�����Զ���������[0��1]֮��ľ��������x��y��������ͼ��ʾ�ij����ͼִ�У���������ʾ���н�������ù˿��н�����������ʾ��лл�������н�����˿��н��ĸ��ʣ�
���𰸡�
��1��
�⣺�����aԪ���Ҹ���bԪ������a��b=10��18��26��34��
��ס��Ҷ��˵ķ��ù��ɵĻ����¼��ռ�Ϊ��
��10��10������10��18������10��26������10��34������18��10������18��18������18��26������18��34����
��26��10������26��18������26��26������26��34������34��10������34��18������34��26������34��34����16������
���У���10��34������18��26������26��18������34��10����4�����η������⣮
�ʡ��ס��Ҷ��˸���֮��Ϊ44Ԫ���ĸ���Ϊ ![]() ��
��
��2��
�⣺����֪0��x��1��0��y��1�㣨x��y����ͼ��������OABC�ڣ�
������ 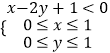 ���õ�������Ϊͼ����Ӱ���֣�
���õ�������Ϊͼ����Ӱ���֣�
��x��2y+1=0����x=0�� ![]() ����x=1��y=1��
����x=1��y=1��
������������������ ![]() ��
��
��˿��н����¼�ΪN����˿��н��ĸ��� ![]() ��
��
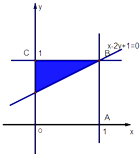
����������1�������aԪ���Ҹ���bԪ������a��b=10��18��26��34���ɴ������оٷ���������ס��Ҷ��˸���֮��Ϊ44Ԫ���ĸ��ʣ���2������֪0��x��1��0��y��1�㣨x��y����������OABC�ڣ��������� 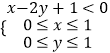 �������ɴ�������˿��н��ĸ��ʣ�
�������ɴ�������˿��н��ĸ��ʣ�
�����㾫�������ճ����ͼ�ǽ����ĸ�������Ҫ֪�������ͼ�ֳ�����ͼ����һ���ù涨��ͼ�Ρ�ָ��������˵����ȷ��ֱ�۵ر�ʾ�㷨��ͼ��;һ�������ͼ�������¼����֣���ʾ��Ӧ�����ij������ͷ�������ߣ���������Ҫ����˵����

 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�����Ŀ��ij��˾Ϊ�˽��û������Ʒ������ȣ���ij�������������100���û����õ��û��Բ�Ʒ�����������Ƶ�ʷֲ������£�
��� | ���� | Ƶ�� | Ƶ�� |
��һ�� | ��50��60] | 10 | 0.1 |
�ڶ��� | ��60��70] | 20 | 0.2 |
������ | ��70��80] | 40 | 0.4 |
������ | ��80��90] | 25 | 0.25 |
������ | ��90��100�� | 5 | 0.05 |
�ϼ� | 100 | 1 |
��1�����������Ƶ�ʷֲ��������Ƹõ����û��Բ�Ʒ����������ֳ���70�ֵĸ��ʣ�
��2������Ƶ�ʷֲ��������ݼ�����������λ����ƽ�����������������������˼�룬��ƽ���ֵ���75�֣���Ϊ�����⣮�жϸõ����û��Բ�Ʒ�Ƿ����⣿