题目内容
12.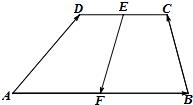 如图,已知梯形ABCD中,AB∥DC,且AB=2CD,E、F分别是DC、AB的中点,设$\overrightarrow{AD}=\overrightarrow a,\overrightarrow{AB}=\overrightarrow b$,试用$\overrightarrow a$、$\overrightarrow b$为基底表示$\overrightarrow{BC}$、$\overrightarrow{EF}$.
如图,已知梯形ABCD中,AB∥DC,且AB=2CD,E、F分别是DC、AB的中点,设$\overrightarrow{AD}=\overrightarrow a,\overrightarrow{AB}=\overrightarrow b$,试用$\overrightarrow a$、$\overrightarrow b$为基底表示$\overrightarrow{BC}$、$\overrightarrow{EF}$.
分析 由题意得到四边形DCBF为平行四边形,再根据向量的向量加法以及几何意义,即可求出答案.
解答 解:∵AB∥DC,AB=2CD,E、F分别是DC、AB的中点,∴DC∥FB,DC=FB,
∴四边形DCBF为平行四边形.
∴$\overrightarrow{BC}=\overrightarrow{FD}=\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}=\overrightarrow a-\frac{1}{2}\overrightarrow b$,
$\overrightarrow{EF}=\overrightarrow{DF}-\overrightarrow{DE}=-\overrightarrow{FD}-\overrightarrow{DE}=-\overrightarrow{BC}-\frac{1}{2}\overrightarrow{DC}=-\overrightarrow a+\frac{1}{2}\overrightarrow b-\frac{1}{4}\overrightarrow b=\frac{1}{4}\overrightarrow b-\overrightarrow a$.
点评 本题考查了向量加法以及几何意义的应用,主要是结合图形和题意对向量进行转化,即用已知向量来表示未知向量.

练习册系列答案
相关题目
7.i10=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
17.已知圆x2+y2=4,直线l:y=x+b,圆上至少有三个点到直线l的距离都是1,则b的取值范围是( )
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | {-$\sqrt{2}$,$\sqrt{2}$} | C. | (-$\sqrt{2}$,$\sqrt{2}$) | D. | [0,$\sqrt{2}$] |
4.下列函数中,是偶函数的是( )
| A. | f(x)=x2 | B. | f(x)=2x | C. | f(x)=x3 | D. | f(x)=$\frac{1}{x}$ |
2.设集合A={x|x=π+$\frac{2kπ}{3}$,k∈z},B={x|x=kπ+$\frac{π}{3}$,k∈z},C={x|x=kπ+$\frac{2π}{3}$,k∈z},则A∩(B∪C)=( )
| A. | $\left\{{x|x=kπ+\frac{π}{3},k∈z}\right\}$ | B. | $\left\{{x|x=kπ-\frac{π}{3},k∈z}\right\}$ | C. | $\left\{{x|x=2kπ±\frac{π}{3},k∈z}\right\}$ | D. | $\left\{{x|x=kπ±\frac{π}{3},k∈z}\right\}$ |