题目内容
20.参数方程$\left\{\begin{array}{l}{x=2sinθ}\\{y=2cosθ}\end{array}\right.$,所表示的曲线为( )| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
分析 利用cos2θ+sin2θ=1即可化简判断出.
解答 解:参数方程$\left\{\begin{array}{l}{x=2sinθ}\\{y=2cosθ}\end{array}\right.$,化为x2+y2=4,
因此次参数方程所表示的曲线为以原点为圆心、2为半径的圆.
故选:B.
点评 本题考查了同角三角函数基本关系式、圆的标准方程,属于基础题.

练习册系列答案
相关题目
15.已知数列{an}、{bn}、{cn}的通项公式分别为:an=n,bn=n(n+1),cn=n(n+1)(n+2),数列{an},{bn}的前n项和分别为S1(n),S2(n),观察下表:
发现S1(n)=$\frac{1}{2}$bn,并可用下面方法证明:
因为ak=k=$\frac{1}{2}[k(k+1)-(k-1)k]$,k=1,2,…n,
所以S1(n)=a1+a2+…an=1+2+…+n=$\frac{1}{2}{(1×2-0×1)+(2×3-1×2)…+[n(n+1)-(n-1)n]}$=$\frac{1}{2}n(n+1)=\frac{1}{2}{b}_{n}$.
(1)指出S2(n)与cn的关系,并类比上面方法证明你的结论;
(2)求和Tn=12+22+…+n2.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| an | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| S1(n) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | … |
| bn | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 | … |
因为ak=k=$\frac{1}{2}[k(k+1)-(k-1)k]$,k=1,2,…n,
所以S1(n)=a1+a2+…an=1+2+…+n=$\frac{1}{2}{(1×2-0×1)+(2×3-1×2)…+[n(n+1)-(n-1)n]}$=$\frac{1}{2}n(n+1)=\frac{1}{2}{b}_{n}$.
(1)指出S2(n)与cn的关系,并类比上面方法证明你的结论;
(2)求和Tn=12+22+…+n2.
15.为了研究某灌溉渠道水的流速y与水深x之间的关系,测得一组数据如下表:
(1)画出散点图,判断变量y与x是否具有相关关系;
(2)若y与x之间具有线性相关关系,求y对x的回归直线方程; ($\sum_{i=1}^5{x_i^2}=16.3$,$\sum_{i=1}^5{{x_i}{y_i}}=18.5$)
(3)预测水深为1.95m水的流速是多少.
参考公式:$b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$$a=\overline y-b\overline x$.
| 水深x(m) | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| 流速y(m/s) | 1 | 1.5 | 2 | 2.5 | 3 |
(2)若y与x之间具有线性相关关系,求y对x的回归直线方程; ($\sum_{i=1}^5{x_i^2}=16.3$,$\sum_{i=1}^5{{x_i}{y_i}}=18.5$)
(3)预测水深为1.95m水的流速是多少.
参考公式:$b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$$a=\overline y-b\overline x$.
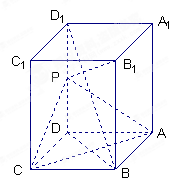 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 如图,已知梯形ABCD中,AB∥DC,且AB=2CD,E、F分别是DC、AB的中点,设$\overrightarrow{AD}=\overrightarrow a,\overrightarrow{AB}=\overrightarrow b$,试用$\overrightarrow a$、$\overrightarrow b$为基底表示$\overrightarrow{BC}$、$\overrightarrow{EF}$.
如图,已知梯形ABCD中,AB∥DC,且AB=2CD,E、F分别是DC、AB的中点,设$\overrightarrow{AD}=\overrightarrow a,\overrightarrow{AB}=\overrightarrow b$,试用$\overrightarrow a$、$\overrightarrow b$为基底表示$\overrightarrow{BC}$、$\overrightarrow{EF}$.