题目内容
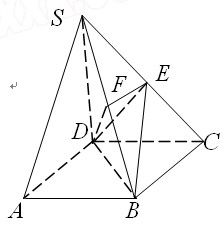
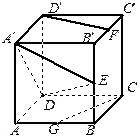
如图3,正方体 中,
中, 分别为
分别为
与 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的正切值.
的正切值.

 中,
中, 分别为
分别为
与
 的中点.
的中点.(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的正切值.
的正切值.
证明:
(I)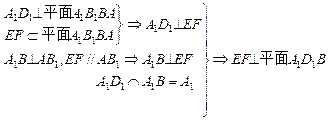
(II)延长DE、CB交于N,∵E为AB中点,∴△DAE≌△NBE
过B作BM⊥EN交于M,连FM,∵FB⊥平面ABCD
∴FM⊥DN,∴∠FMB为二面角F—DE—C的平面角
设AB=a,则BM=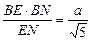 又BF=
又BF=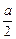
∴tan∠FMB=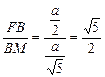 ,即二面角F—DE—C大小的正切值为
,即二面角F—DE—C大小的正切值为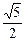
(I)
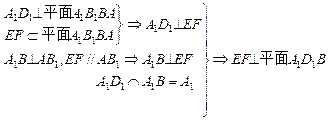
(II)延长DE、CB交于N,∵E为AB中点,∴△DAE≌△NBE
过B作BM⊥EN交于M,连FM,∵FB⊥平面ABCD
∴FM⊥DN,∴∠FMB为二面角F—DE—C的平面角
设AB=a,则BM=
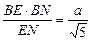 又BF=
又BF=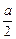
∴tan∠FMB=
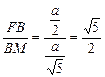 ,即二面角F—DE—C大小的正切值为
,即二面角F—DE—C大小的正切值为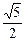
略

练习册系列答案
相关题目
 中,
中,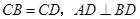 ,点
,点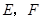 分别是
分别是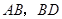 的中点. 求证:
的中点. 求证: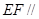 平面
平面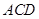 ;
;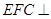 平面
平面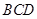 .
.
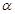 的一条斜线有一个平面与平面
的一条斜线有一个平面与平面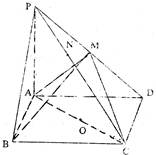
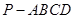 中,底面
中,底面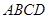 是
是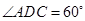 的菱形,
的菱形, 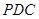 是边长为2的正三角形,且与底面
是边长为2的正三角形,且与底面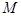 为
为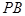 的中点.
的中点.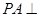 平面
平面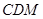 ;
;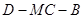 的余弦值.
的余弦值.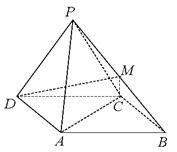
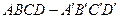 棱长为1,
棱长为1,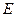 是
是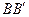 的中点,
的中点,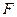 是
是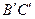 的中点,
的中点,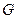 是
是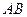 的中点
的中点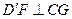
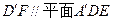 ;
;
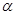 、
、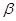 、
、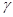 和直线
和直线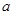 、
、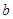 、m、n,下列命题中真命题是( )
、m、n,下列命题中真命题是( ) ,则
,则
 ,则
,则
 ,则
,则
 则
则
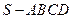 中,底面
中,底面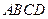 为正方形,侧棱
为正方形,侧棱
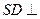 底面
底面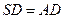 ,
,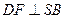 垂足为
垂足为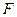 ,
,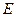 是
是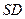 的中点.
的中点. Ⅰ)证明:
Ⅰ)证明: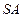 ∥平面
∥平面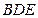 ;
;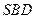 ⊥平面
⊥平面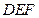 .
.