题目内容
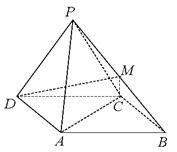
如图,四棱锥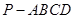 中,底面
中,底面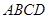 是
是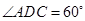 的菱形,
的菱形,
侧面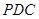 是边长为2的正三角形,且与底面
是边长为2的正三角形,且与底面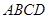 垂直,
垂直,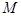 为
为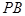 的中点.
的中点.
(1)求证: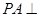 平面
平面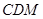 ;
;
(2)求二面角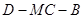 的余弦值.
的余弦值.
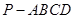 中,底面
中,底面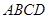 是
是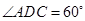 的菱形,
的菱形, 侧面
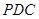 是边长为2的正三角形,且与底面
是边长为2的正三角形,且与底面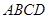 垂直,
垂直,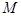 为
为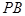 的中点.
的中点.(1)求证:
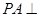 平面
平面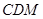 ;
;(2)求二面角
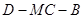 的余弦值.
的余弦值.
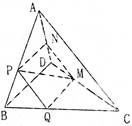
由底面ABCD为菱形且∠ADC=60°,DC=2,DO=1,有OA⊥DC. 分别以OA、OC、OP所在直线为x、y、z轴,建立空间直角坐标系如图,
则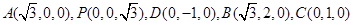 。
。
(1) 由M为PB中点, ∴
∴
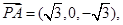
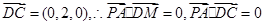 ,
,
∴PA⊥DM,PA⊥DC. ∴PA⊥平面DMC.……………6分
(2)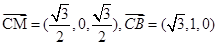 ,设平面BMC的法向量
,设平面BMC的法向量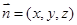 ,
,
则由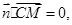 可得
可得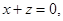 由
由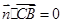 可得
可得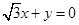 ,取
,取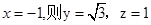 。
。
所以可取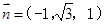 。由(Ⅰ)知平面CDM的法向量可取
。由(Ⅰ)知平面CDM的法向量可取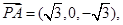 ……9分
……9分
 。又易知二面角
。又易知二面角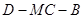 为钝二面角.
为钝二面角.
∴二面角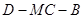 的余弦值为
的余弦值为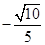
则
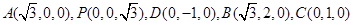 。
。(1) 由M为PB中点,
 ∴
∴
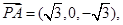
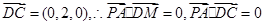 ,
,∴PA⊥DM,PA⊥DC. ∴PA⊥平面DMC.……………6分
(2)
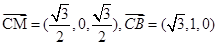 ,设平面BMC的法向量
,设平面BMC的法向量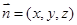 ,
,则由
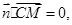 可得
可得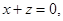 由
由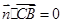 可得
可得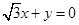 ,取
,取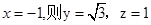 。
。所以可取
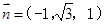 。由(Ⅰ)知平面CDM的法向量可取
。由(Ⅰ)知平面CDM的法向量可取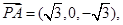 ……9分
……9分 。又易知二面角
。又易知二面角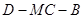 为钝二面角.
为钝二面角.∴二面角
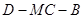 的余弦值为
的余弦值为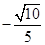
略

练习册系列答案
相关题目
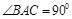 ,
,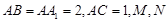 分别是
分别是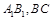 的中点。 (Ⅰ)证明:
的中点。 (Ⅰ)证明: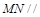 平面
平面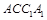 ;
;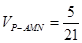 ,求
,求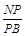 的值
的值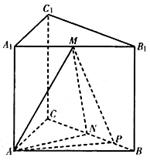
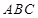 的边长为4,
的边长为4,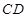 是
是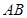 边上的高,
边上的高,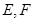 分别是
分别是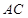
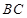 边的中点,现将△
边的中点,现将△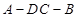 .
.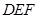 的位置关系,并说明理由;
的位置关系,并说明理由;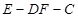 的余弦值;
的余弦值; ,使
,使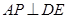 ?证明你的结论.
?证明你的结论.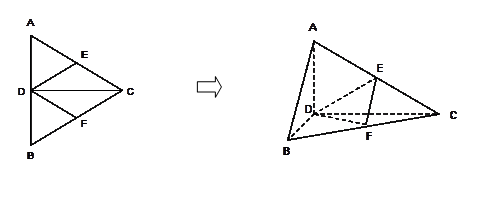
 中,
中, 分别为
分别为
 的中点.
的中点. 平面
平面 ;
; 的正切值.
的正切值.
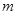 、
、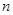 是不同的直线,
是不同的直线,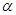 、
、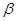 是不同的平面,有下列命题:
是不同的平面,有下列命题: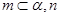 ∥
∥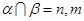 ∥
∥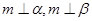 ,则
,则 个
个 个
个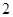 个
个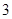 个
个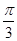 ,另一直线与这个平面所成的角是
,另一直线与这个平面所成的角是 。则这
。则这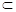 β,则下面四个命题:
β,则下面四个命题: