题目内容
设函数f1(x)=log2x-(
)x,f2(x)=log
x-(
)x的零点分别为x1,x2,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A.0<x1x2<1 | B.x1x2=1 | C.1<x1x2<2 | D.x1x2≥2 |
解析:令f1(x)=0得:log2x=(
)x,令f2(x)=0得:log
x=(
)x,
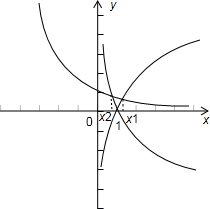
分别画出左右两边函数的图象,如图所示.
由指数与对数函数的图象知:x1>1>x2>0,
于是有lo
=(
)x1<(
)x2=lo
=lo
,得x1<
,
故选A.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
分别画出左右两边函数的图象,如图所示.
由指数与对数函数的图象知:x1>1>x2>0,
于是有lo
| g | x12 |
| 1 |
| 2 |
| 1 |
| 2 |
| g | x2
|
| g |
|
| 1 |
| x2 |
故选A.


练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
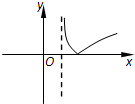
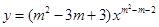 的图像不过坐标原点,则
的图像不过坐标原点,则 的值是___ .
的值是___ .