题目内容
已知an=log（n+2）（n+3），我们把使乘积a1•a2•a3•…•an为整数的数n称为“优数”，则在区间（0，2012）内所有优数的个数为（ ）
| A．3 | B．4 | C．5 | D．6 |
由an=log（n+2）（n+3），
∴a1•a2•a3•…•an=log34•log45…logn+2（n+3）=
•
•
…
=
=log3（n+3）．
∵a1•a2•a3•…•an为整数，
∴n+3是3的k次方（k∈Z）．
∴n+3可取 9，27，81，243，729．
则n在区间（0，2012）内可取 6，24，78，240，726．
∴在区间（0，2012）内所有“优数”的个数为5．
故选：C．
∴a1•a2•a3•…•an=log34•log45…logn+2（n+3）=
| lg4 |
| lg3 |
| lg5 |
| lg4 |
| lg6 |
| lg5 |
| lg(n+3) |
| lg(n+2) |
| lg(n+3) |
| lg3 |
∵a1•a2•a3•…•an为整数，
∴n+3是3的k次方（k∈Z）．
∴n+3可取 9，27，81，243，729．
则n在区间（0，2012）内可取 6，24，78，240，726．
∴在区间（0，2012）内所有“优数”的个数为5．
故选：C．
练习册系列答案
相关题目
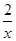且f(4)＝
.
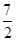