题目内容
已知函数f(x)=log
sin(x-
).
(1)求它的定义域,值域;
(2)判定它的奇偶性和周期性;
(3)判定它的单调区间及每一区间上的单调性.
| 1 |
| 2 |
| 2 |
| π |
| 4 |
(1)求它的定义域,值域;
(2)判定它的奇偶性和周期性;
(3)判定它的单调区间及每一区间上的单调性.
(1)要使函数有意义,则
sin(x-
)>0,解得2kπ<x-
<2kπ+π,
即2kπ+
<x<2kπ+
,
即函数的定义域为(2kπ+
,2kπ+
),
∵0<
sin?(x-
)≤1,
∴函数f(x)=log
sin(x-
)≥0,
即函数的值域为[0,+∞).
(2)∵函数的定义域关于原点不对称,∴函数为非奇非偶函数函数.
∵函数y=
sin?(x-
)的周期是π,
∴函数f(x)=log
sin(x-
)周期是π.
(3)∵y=
sin?(x-
)的单调递增区间为(2kπ+
,2kπ+
],
∴根据复合函数的单调性可知此时函数f(x)=log
sin(x-
)单调递减.
∵y=
sin?(x-
)的单调递减区间为[2kπ+
2kπ+
),
∴根据复合函数的单调性可知此时函数f(x)=log
sin(x-
)单调递增.
故函数的单调递增区间为为[2kπ+
2kπ+
),递减区间为为(2kπ+
,2kπ+
].
| 2 |
| π |
| 4 |
| π |
| 4 |
即2kπ+
| π |
| 4 |
| 5π |
| 4 |
即函数的定义域为(2kπ+
| π |
| 4 |
| 5π |
| 4 |
∵0<
| 2 |
| π |
| 4 |
∴函数f(x)=log
| 1 |
| 2 |
| 2 |
| π |
| 4 |
即函数的值域为[0,+∞).
(2)∵函数的定义域关于原点不对称,∴函数为非奇非偶函数函数.
∵函数y=
| 2 |
| π |
| 4 |
∴函数f(x)=log
| 1 |
| 2 |
| 2 |
| π |
| 4 |
(3)∵y=
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴根据复合函数的单调性可知此时函数f(x)=log
| 1 |
| 2 |
| 2 |
| π |
| 4 |
∵y=
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
∴根据复合函数的单调性可知此时函数f(x)=log
| 1 |
| 2 |
| 2 |
| π |
| 4 |
故函数的单调递增区间为为[2kπ+
| 3π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
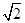 ),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.