题目内容
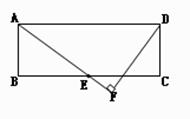
(12分)如图,矩形ABCD中,E是BC中点,DF⊥AE交AE延长线于F,AB="a" ,BC=b,
求证:DF=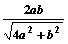

求证:DF=
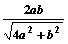
证明:见解析。
此题综合运用了平行四边形的性质和平行线分线段成比例定理.
要求DF的长,根据平行四边形的性质,知CD=AB=6,只需求得CF的长,再根据AB∥CD,得CF:AB
="CE" :BE ,即可求解.
证明:在矩形ABCD中,AD=BC=b,AD∥BC,∴∠DAF=∠BEA
∵∠B=∠AFD=90º,∴△ABE∽△DFA,∴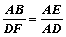 ……4分
……4分
∵E是BC的中点,∴BE=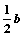 ……………
……………
在Rt△ABE中,AE=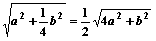
∴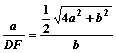 ,∴DF=
,∴DF=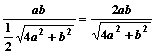 ………..12分
………..12分
要求DF的长,根据平行四边形的性质,知CD=AB=6,只需求得CF的长,再根据AB∥CD,得CF:AB
="CE" :BE ,即可求解.
证明:在矩形ABCD中,AD=BC=b,AD∥BC,∴∠DAF=∠BEA
∵∠B=∠AFD=90º,∴△ABE∽△DFA,∴
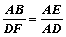 ……4分
……4分∵E是BC的中点,∴BE=
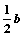 ……………
……………在Rt△ABE中,AE=
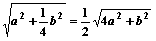
∴
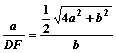 ,∴DF=
,∴DF=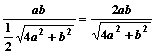 ………..12分
………..12分
练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
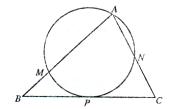
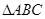 ,过顶点
,过顶点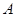 的圆与边
的圆与边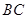 切于
切于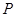 ,与边
,与边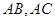 分别交于点
分别交于点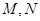 ,且
,且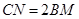 ,点
,点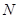 平分
平分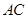 .求证:
.求证: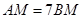 .
.
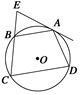
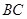 与
与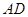 的延长线交于点
的延长线交于点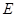 ,点
,点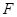 在
在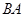 的延长线上.
的延长线上.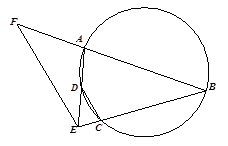
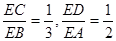 ,求
,求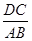 的值;
的值;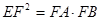 ,证明:
,证明: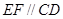 .
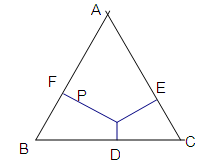
.
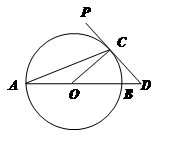
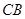 是⊙
是⊙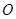 的直径,
的直径,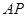 是⊙
是⊙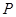 ,
,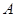 为切点.若
为切点.若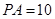 ,
,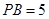 ,
,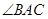 的平分线
的平分线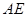 与
与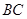 和⊙
和⊙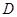 、
、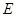 ,则
,则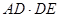 的值为( )
的值为( )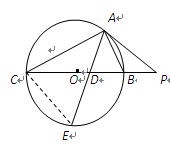
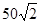
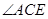 =
=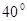 ,
,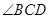 = .
= . 