题目内容
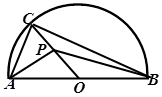
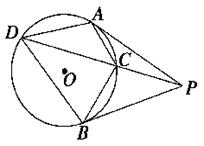
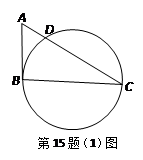
(本小题12分)如图,四边形ABCD内接于⊙O,AB=AD过A点的切线交CB的延长线于E点.求证:AB2=BE·CD.

见解析.
利用连结AC.∵EA切⊙O于A,∴∠EAB=∠ACB,
∵AB=AD,∴∠ACD=∠ACB,AB=AD.∴∠EAB=∠ACD.
又四边形ABCD内接于⊙O,所以∠ABE=∠D.
∴△ABE∽△CDA.
∴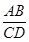 =
=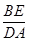 ,即AB·DA=BE·CD.
,即AB·DA=BE·CD.
∴AB2=BE·CD
证明 连结AC.
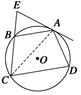
∵EA切⊙O于A,∴∠EAB=∠ACB,
∵AB=AD,
∴∠ACD=∠ACB,AB=AD.
∴∠EAB=∠ACD.
又四边形ABCD内接于⊙O,
所以∠ABE=∠D.
∴△ABE∽△CDA.
∴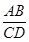 =
=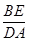 ,即AB·DA=BE·CD.
,即AB·DA=BE·CD.
∴AB2=BE·CD.
∵AB=AD,∴∠ACD=∠ACB,AB=AD.∴∠EAB=∠ACD.
又四边形ABCD内接于⊙O,所以∠ABE=∠D.
∴△ABE∽△CDA.
∴
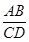 =
=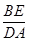 ,即AB·DA=BE·CD.
,即AB·DA=BE·CD.∴AB2=BE·CD
证明 连结AC.

∵EA切⊙O于A,∴∠EAB=∠ACB,
∵AB=AD,
∴∠ACD=∠ACB,AB=AD.
∴∠EAB=∠ACD.
又四边形ABCD内接于⊙O,
所以∠ABE=∠D.
∴△ABE∽△CDA.
∴
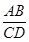 =
=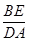 ,即AB·DA=BE·CD.
,即AB·DA=BE·CD.∴AB2=BE·CD.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
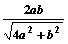
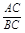 =
=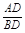 .
.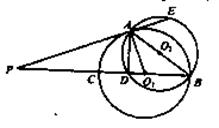
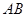 和
和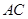 是圆的两条弦,过点
是圆的两条弦,过点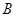 作圆的切线与
作圆的切线与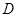 .过点
.过点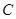 作
作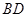 的平行线与圆交于点
的平行线与圆交于点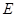 ,与
,与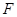 ,
,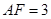 ,
,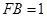 ,
,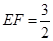 ,则线段
,则线段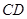 的长为 .
的长为 .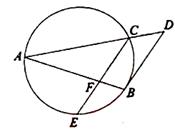
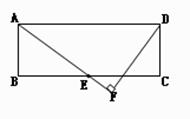
 以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE, AE交⊙O于点F
以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE, AE交⊙O于点F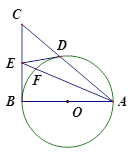
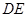 是⊙O的切线;
是⊙O的切线;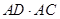 的值.
的值.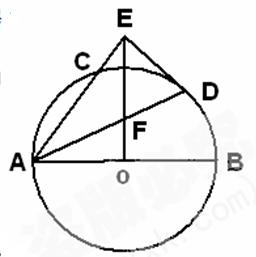

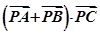 的最小值为 .
的最小值为 .