题目内容
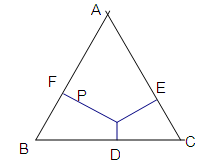
如图,△ABC是边长为12的等边三角形,点P是三角形内的一点,过P分别作边BC,CA,AB的垂线,垂足分别为D,E,F.已知PD:PE:PF=1:2:3,那么四边形BDPF的面积是 .

11

连接AP,BP,CP,作FG⊥BC于G,PH∥BC,交FG于H,
∵PD,PE,PF分别垂直于BC,AC,AB,
∴S△ABP+S△APC+S△BPC= (PD×12+PE×12+PF×12)=S△ABC=36
(PD×12+PE×12+PF×12)=S△ABC=36 又∵PD:PE:PF=1:2:3,∴PD=
又∵PD:PE:PF=1:2:3,∴PD= ,PF=3
,PF=3 ,∵∠FPH=30°∴FH=
,∵∠FPH=30°∴FH= ,FG=
,FG= ,GD=HP=
,GD=HP= ,又∵BG=
,又∵BG= ,∴S四边形BDPF=S△BFG+S梯形FGDP=
,∴S四边形BDPF=S△BFG+S梯形FGDP= FG•BG+
FG•BG+ (FG+PD)•GD=11
(FG+PD)•GD=11
∵PD,PE,PF分别垂直于BC,AC,AB,
∴S△ABP+S△APC+S△BPC=
 (PD×12+PE×12+PF×12)=S△ABC=36
(PD×12+PE×12+PF×12)=S△ABC=36 又∵PD:PE:PF=1:2:3,∴PD=
又∵PD:PE:PF=1:2:3,∴PD= ,PF=3
,PF=3 ,∵∠FPH=30°∴FH=
,∵∠FPH=30°∴FH= ,FG=
,FG= ,GD=HP=
,GD=HP= ,又∵BG=
,又∵BG= ,∴S四边形BDPF=S△BFG+S梯形FGDP=
,∴S四边形BDPF=S△BFG+S梯形FGDP= FG•BG+
FG•BG+ (FG+PD)•GD=11
(FG+PD)•GD=11

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
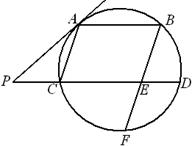
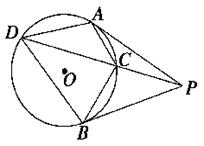
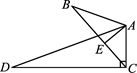
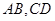 是圆的两条平行弦,
是圆的两条平行弦,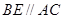 ,
,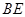 交
交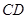 于
于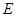 、交圆于
、交圆于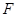 ,过
,过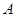 点的切线交
点的切线交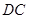 的延长线于
的延长线于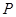 ,
,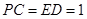 ,
,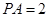 .
.
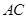 的长;
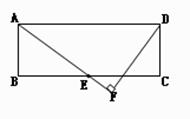
的长;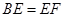 .
.
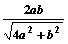
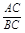 =
=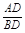 .
.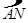 折叠过来和直径MN交于点B,如
折叠过来和直径MN交于点B,如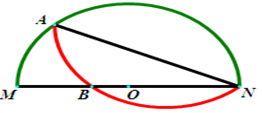
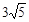
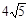
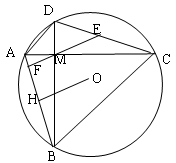
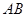 为⊙
为⊙ 的直径,
的直径,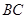 切⊙
切⊙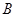 ,
,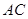 交⊙
交⊙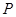 ,
,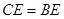 ,点
,点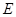 在
在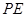 是⊙
是⊙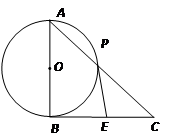
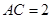 ,则BD等于 .
,则BD等于 .