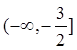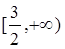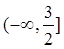题目内容
(16分)已知函数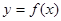 是定义在
是定义在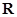 上的奇函数,且当
上的奇函数,且当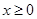 时,
时,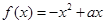 .
.
(1)当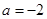 时,求函数
时,求函数 的解析式;
的解析式;
(2)若函数 为单调递减函数;
为单调递减函数;
①直接写出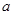 的范围(不必证明);
的范围(不必证明);
②若对任意实数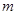 ,
,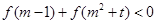 恒成立,求实数
恒成立,求实数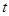 的取值范围.
的取值范围.
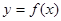 是定义在
是定义在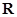 上的奇函数,且当
上的奇函数,且当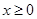 时,
时,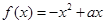 .
.(1)当
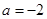 时,求函数
时,求函数 的解析式;
的解析式;(2)若函数
 为单调递减函数;
为单调递减函数; ①直接写出
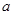 的范围(不必证明);
的范围(不必证明);②若对任意实数
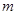 ,
,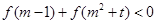 恒成立,求实数
恒成立,求实数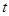 的取值范围.
的取值范围.(1)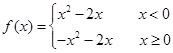 ;(2)
;(2)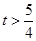 。
。
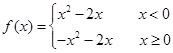 ;(2)
;(2)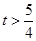 。
。本试题主要是考查了抽象函数的解析式的求解和单调性的证明以及解不等式。
(1)因为当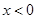 时,
时,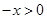 ,又因为
,又因为 为奇函数,所以
为奇函数,所以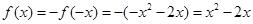 ,进而得到解析式。
,进而得到解析式。
(2)根据函数单调性,对于参数a分为正负来讨论得到取值范围。
(3)因为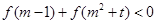 ,∴
,∴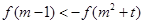
所以 是奇函数,∴
是奇函数,∴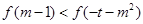 ,而又因为
,而又因为 为
为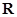 上的单调递减函数,所以
上的单调递减函数,所以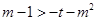 恒成立,分离参数的思想得到范围。
恒成立,分离参数的思想得到范围。
(1)当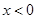 时,
时,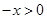 ,又因为
,又因为 为奇函数,
为奇函数,
所以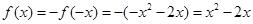
所以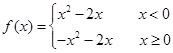 …………………………6分
…………………………6分
(2)①当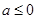 时,对称轴
时,对称轴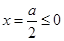 ,所以
,所以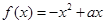 在
在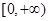 上单调递减,
上单调递减,
由于奇函数关于原点对称的区间上单调性相同,所以 在
在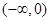 上单调递减,
上单调递减,
又在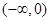 上
上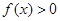 ,在
,在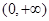 上
上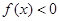 ,
,
所以当a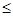 0时,
0时,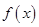 为R上的单调递减函数
为R上的单调递减函数
当a>0时,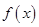 在
在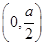 上递增,在
上递增,在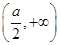 上递减,不合题意
上递减,不合题意
所以函数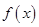 为单调函数时,a的范围为a
为单调函数时,a的范围为a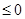 ………………………………………….10分
………………………………………….10分
②因为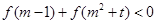 ,∴
,∴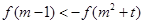
所以 是奇函数,∴
是奇函数,∴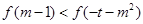 …………………………12分
…………………………12分
又因为 为
为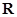 上的单调递减函数,所以
上的单调递减函数,所以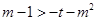 恒成立,…………………14分
恒成立,…………………14分
所以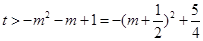 恒成立, 所以
恒成立, 所以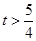 …………………………16分
…………………………16分
(1)因为当
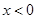 时,
时,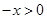 ,又因为
,又因为 为奇函数,所以
为奇函数,所以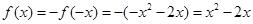 ,进而得到解析式。
,进而得到解析式。(2)根据函数单调性,对于参数a分为正负来讨论得到取值范围。
(3)因为
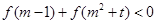 ,∴
,∴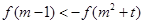
所以
 是奇函数,∴
是奇函数,∴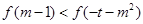 ,而又因为
,而又因为 为
为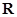 上的单调递减函数,所以
上的单调递减函数,所以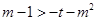 恒成立,分离参数的思想得到范围。
恒成立,分离参数的思想得到范围。(1)当
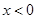 时,
时,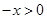 ,又因为
,又因为 为奇函数,
为奇函数,所以
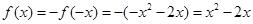
所以
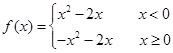 …………………………6分
…………………………6分(2)①当
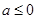 时,对称轴
时,对称轴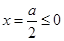 ,所以
,所以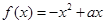 在
在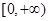 上单调递减,
上单调递减,由于奇函数关于原点对称的区间上单调性相同,所以
 在
在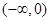 上单调递减,
上单调递减,又在
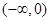 上
上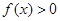 ,在
,在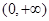 上
上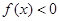 ,
,所以当a
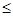 0时,
0时,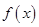 为R上的单调递减函数
为R上的单调递减函数当a>0时,
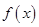 在
在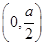 上递增,在
上递增,在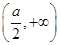 上递减,不合题意
上递减,不合题意所以函数
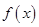 为单调函数时,a的范围为a
为单调函数时,a的范围为a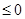 ………………………………………….10分
………………………………………….10分②因为
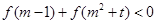 ,∴
,∴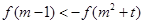
所以
 是奇函数,∴
是奇函数,∴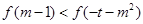 …………………………12分
…………………………12分又因为
 为
为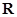 上的单调递减函数,所以
上的单调递减函数,所以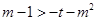 恒成立,…………………14分
恒成立,…………………14分所以
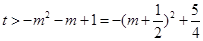 恒成立, 所以
恒成立, 所以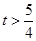 …………………………16分
…………………………16分
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
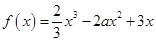 (
(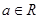 ).
).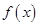 的单调区间;
的单调区间;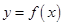 在
在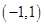 内有且只有一个极值点, 求a的取值范围.
内有且只有一个极值点, 求a的取值范围.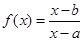 在区间
在区间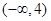 上是增函数,则有( )
上是增函数,则有( )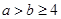
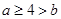
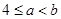
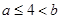
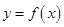 是定义在R上的减函数,且
是定义在R上的减函数,且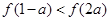 ,
,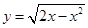 的单调递减区间是 __________________.
的单调递减区间是 __________________.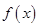 是定义在
是定义在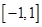 上的单调递增函数,且
上的单调递增函数,且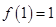
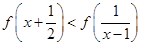
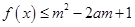 ,对所有
,对所有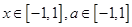 恒成立,求实数
恒成立,求实数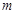 的取值范围。
的取值范围。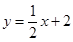 ,则
,则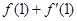 = .
= . 上是减函数,则实数a的取值范围是 ( )
上是减函数,则实数a的取值范围是 ( )