题目内容
(12分)已知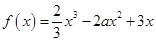 (
(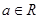 ).
).
⑴求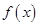 的单调区间;
的单调区间;
⑵若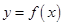 在
在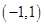 内有且只有一个极值点, 求a的取值范围.
内有且只有一个极值点, 求a的取值范围.
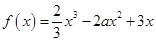 (
(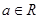 ).
).⑴求
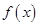 的单调区间;
的单调区间;⑵若
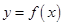 在
在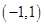 内有且只有一个极值点, 求a的取值范围.
内有且只有一个极值点, 求a的取值范围.⑴①当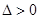 时,
时,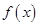 在
在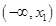 和
和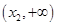 单调递增,在
单调递增,在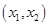 单调递减;
单调递减;
②当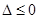 时,
时,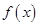 单调递增;⑵
单调递增;⑵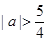 .
.
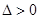 时,
时,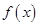 在
在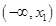 和
和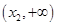 单调递增,在
单调递增,在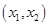 单调递减;
单调递减;②当
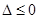 时,
时,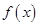 单调递增;⑵
单调递增;⑵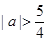 .
.试题分析:(1)先求出导函数f'(x),根据函数f(x)在区间(0,
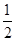 )上单调递增,在区间(
)上单调递增,在区间( 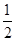 ,1)上单调递减,可知x=
,1)上单调递减,可知x=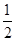 是函数的极值,从而f'(
是函数的极值,从而f'(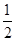 )=0,解之即可求出m的值;
)=0,解之即可求出m的值;(2)本小问由
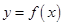 在
在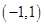 上只有一个极值点,知
上只有一个极值点,知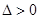 ,即
,即 ;且要满足
;且要满足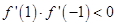 得到参数a的范围。
得到参数a的范围。解:⑴
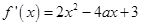 ,
,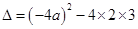 ;
;①当
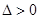 时,即
时,即 时,方程
时,方程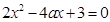 有两个根,
有两个根,分别为
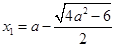 ,
,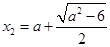 ;故
;故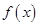 在
在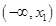 和
和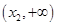 单调递增,在
单调递增,在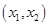 单调递减;
单调递减;②当
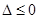 时,
时,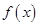 单调递增;
单调递增;⑵由
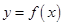 在
在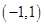 上只有一个极值点,知
上只有一个极值点,知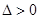 ,即
,即 ;
;且要满足
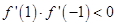 ,解得
,解得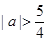 ,综合得
,综合得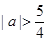 .
.点评:解决该试题的关键是利用导数得到函数的单调去甲,以及函数的极值,进而得到从那数m的值,同时对于极值点的问题,利用判别式和区间端点的函数值的符号来判定得到。

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
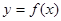 是定义在
是定义在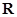 上的奇函数,且当
上的奇函数,且当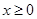 时,
时,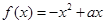 .
.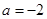 时,求函数
时,求函数 的解析式;
的解析式;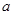 的范围(不必证明);
的范围(不必证明);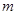 ,
,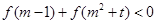 恒成立,求实数
恒成立,求实数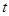 的取值范围.
的取值范围.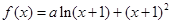 在
在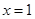 处有极值.
处有极值.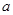 值;
值;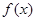 的单调区间;
的单调区间;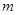 ,使得不等式
,使得不等式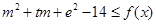 对任意
对任意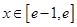 及
及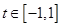
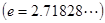
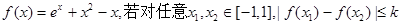 恒成立,则k的取值范围为 。
恒成立,则k的取值范围为 。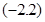 上的奇函数
上的奇函数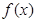 ,满足
,满足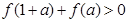 ,又当
,又当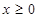 时,
时,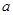 的取值范围。
的取值范围。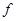 (
(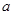 *b)=
*b)=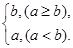 则函数
则函数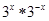 )的值域是( )
)的值域是( ) 的值域是 .
的值域是 .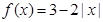 ,
,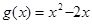 ,
,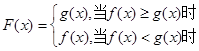 ,则
,则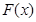 的最值是( )
的最值是( )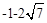
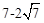 ,无最小值
,无最小值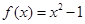 ,对任意
,对任意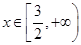 ,
,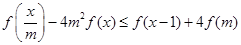 恒成立,则实数
恒成立,则实数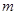 的取值范围是
的取值范围是