题目内容
16.已知数列{an}的前n项和为Sn,且满足Sn=(-1)nan+$\frac{1}{{2}^{n}}$,设{Sn}的前n项和为Tn,则T2016=$\frac{1}{3}$•$\frac{{2}^{2016}-1}{{2}^{2016}}$.分析 通过Sn=(-1)nan+$\frac{1}{{2}^{n}}$可知a1=$\frac{1}{4}$、当n≥2时an=Sn-Sn-1=(-1)nan+$\frac{1}{{2}^{n}}$-(-1)n-1an-1-$\frac{1}{{2}^{n-1}}$,分n为奇数、偶数两种情况讨论可知an=$\frac{1}{{2}^{n+1}}$(n为奇数)、an=-$\frac{1}{{2}^{n}}$(n为偶数),进而计算可得结论.
解答 解:∵Sn=(-1)nan+$\frac{1}{{2}^{n}}$,
∴当n=1时,a1=-a1+$\frac{1}{2}$,即a1=$\frac{1}{4}$;
∴当n≥2时,an=Sn-Sn-1=(-1)nan+$\frac{1}{{2}^{n}}$-(-1)n-1an-1-$\frac{1}{{2}^{n-1}}$,
∴当n为偶数时,an=an+an-1-$\frac{1}{{2}^{n}}$,即an-1=$\frac{1}{{2}^{n}}$,
∴an=$\frac{1}{{2}^{n+1}}$(n为奇数);
当n为奇数时,an=-an-an-1-$\frac{1}{{2}^{n}}$,即2an=-an-1-$\frac{1}{{2}^{n}}$,
∴2•$\frac{1}{{2}^{n+1}}$=-an-1+$\frac{1}{{2}^{n-1}}$,即an-1=-$\frac{1}{{2}^{n-1}}$,
∴an=-$\frac{1}{{2}^{n}}$(n为偶数);
综上所述,an=$\left\{\begin{array}{l}{\frac{1}{{2}^{n+1}},}&{n为奇数}\\{-\frac{1}{{2}^{n}},}&{n为偶数}\end{array}\right.$;
∴T2016=(-a1+a2-a3+a4-…-a2015+a2016)+($\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{2016}}$)
=(-a1+a2)+(-a3+a4)+…+(-a2015+a2016)+($\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{2016}}$)
=(-$\frac{1}{{2}^{2}}$-$\frac{1}{{2}^{2}}$)+(-$\frac{1}{{2}^{4}}$-$\frac{1}{{2}^{4}}$)+…+(-$\frac{1}{{2}^{2016}}$-$\frac{1}{{2}^{2016}}$)+$\frac{\frac{1}{2}(1-\frac{1}{{2}^{2016}})}{1-\frac{1}{2}}$
=-2($\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{2016}}$)+1-$\frac{1}{{2}^{2016}}$
=-2•$\frac{\frac{1}{{2}^{2}}×(1-\frac{1}{{2}^{2×1008}})}{1-\frac{1}{{2}^{2}}}$+1-$\frac{1}{{2}^{2016}}$
=$\frac{1}{3}$•$\frac{{2}^{2016}-1}{{2}^{2016}}$,
故答案为:$\frac{1}{3}$•$\frac{{2}^{2016}-1}{{2}^{2016}}$.
点评 本题考查了数列的求和,考查了数列的函数特性,解答此题的关键在于当n为偶数时能求出奇数项的通项,当n为奇数时求出偶数项的通项,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案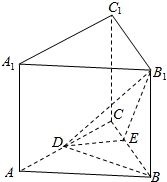 在正三棱柱ABC-A1B1C1中,AB=4,AA1=3,点D是AC的中点,点E在棱BC上(不含端点),且DE⊥B1E.
在正三棱柱ABC-A1B1C1中,AB=4,AA1=3,点D是AC的中点,点E在棱BC上(不含端点),且DE⊥B1E.