Question

4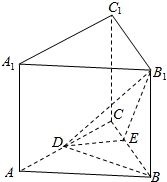．在正三棱柱ABC-A₁B₁C₁中，AB=4，AA₁=3，点D是AC的中点，点E在棱BC上（不含端点），且DE⊥B₁E．
（Ⅰ）求证：平面B₁DE⊥平面BCC₁B₁；
（Ⅱ）求直线BD与平面B₁DE所成角的正弦值．

Answer 1

分析 （Ⅰ）通过证明DE⊥平面BCC₁B₁，利用平面与平面垂直的判定定理证明平面B₁DE⊥平面BCC₁B₁；
（Ⅱ）作BH⊥B₁E于H，连结DH，说明∠BDH是直线BD与平面B₁DE所成角，在Rt△BDH中，求解直线与平面所成角的正弦函数值．

解答 解：（Ⅰ）证明：由三棱柱ABC-A₁B₁C₁的性质可知CC₁⊥平面ABC，
又DE?平面ABC，故CC₁⊥DE，
又DE⊥B₁E，所以DE⊥平面BCC₁B₁，
又因为DE?平面B₁DE，
所以平面B₁DE⊥平面BCC₁B₁；
（Ⅱ）作BH⊥B₁E于H，连结DH，
由（Ⅰ）得平面B₁DE⊥平面BCC₁B₁；
故BH⊥平面B₁DE，
故∠BDH是直线BD与平面B₁DE所成角，
又因为△BDH为边长为4的正三角形，点D是AC的中点，得CD=2，
又由于BB₁=AA₁=3，
所以△EBB₁为等腰三角形，HB=$\frac{3}{\sqrt{2}}$．
又BD=2$\sqrt{3}$，在Rt△BDH中，$sin∠BDH=\frac{HB}{DB}=\frac{\sqrt{6}}{4}$．

点评 本题考查直线与平面所成角的求法，平面与平面垂直的判定定理的应用，考查空间想象能力以及计算能力．