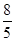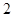题目内容
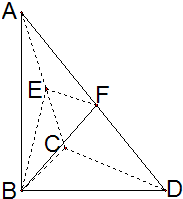
正方形ABCD的边长为1，分别取BC、CD的中点E、F，连接AE、EF、AF，以AE、EF、FA为折痕，折叠这个正方形，使B、C、D重合为一点P，得到一个四面体P-AEF，
（1）求证：AP⊥EF；
（2）求证：平面APE⊥平面APF．
（1）求证：AP⊥EF；
（2）求证：平面APE⊥平面APF．
证明：（1）因为∠APE=∠APF=90°，
PE∩PF=P．所以PA⊥平面PEF，
因为EF?平面PEF，所以PA⊥EF；
（2）因为∠APE=∠APF=90°，
PA∩PF=P．所以PE⊥平面APF，
又PE?平面APE，所以平面APE⊥平面APF．
PE∩PF=P．所以PA⊥平面PEF，
因为EF?平面PEF，所以PA⊥EF；
（2）因为∠APE=∠APF=90°，
PA∩PF=P．所以PE⊥平面APF，
又PE?平面APE，所以平面APE⊥平面APF．
练习册系列答案
阅读快车系列答案
相关题目
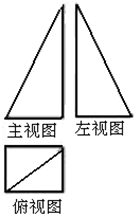
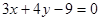和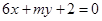
的距离是( )
