题目内容
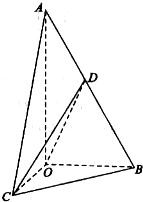
如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2
,动点D在线段AB上.
(Ⅰ)求证:平面COD⊥平面AOB;
(Ⅱ)当点D运动到线段AB的中点时,求二面角D-CO-B的大小;
(Ⅲ)当CD与平面AOB所成角最大时,求三棱锥C-OBD的体积.
| 2 |
(Ⅰ)求证:平面COD⊥平面AOB;
(Ⅱ)当点D运动到线段AB的中点时,求二面角D-CO-B的大小;
(Ⅲ)当CD与平面AOB所成角最大时,求三棱锥C-OBD的体积.

(Ⅰ)证明:∵AO⊥底面BOC,∴AO⊥OC,AO⊥OB.
∵∠OAB=∠OAC=30°,AB=AC=4,∴OC=OB=2.(2分)
∵BC=2
| 2 |
∵OC?平面COD,∴平面COD⊥平面AOB.(5分)
(Ⅱ):由(Ⅰ)知OC⊥平面AOB,
∴OC⊥OB,OC⊥OD,
∴∠DOB是二面角D-CO-B的平面角.(7分)
∵D为AB的中点,∴OD=2,BD=2,
又OB=2,∴∠DOB=60°,
∴二面角D-CO-B的大小为60°.(9分)
(Ⅲ):∵OC⊥平面AOB,CD交平面AOB于D,
∴∠CDO是CD与平面AOB所成角.(10分)
tan∠CDO=
| OC |
| OD |
| 2 |
| OD |
∴取OD⊥AB,OD=
| 3 |
∴VC-OBD=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
即CD与平面AOB所成角最大时,三棱锥C-OBD的体积为
| ||
| 3 |

练习册系列答案
相关题目
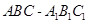 中,
中,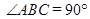 ,
,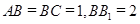 ,求:
,求: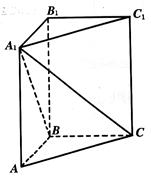
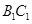 与
与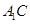 所成角的大小;
所成角的大小; 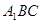 的距离.
的距离.