题目内容
2.下列4个命题:①“如果x+y=0,则x、y互为相反数”的逆命题
②“如果x2+x-6≥0,则x>2”的否命题
③在△ABC中,“A>30°”是“$sinA>\frac{1}{2}$”的充分不必要条件
④“函数f(x)=tan(x+φ)为奇函数”的充要条件是“φ=kπ(k∈Z)”
其中真命题的序号是①.
分析 对于①:先求得逆命题,再判断真假,由相反数的定义易知①正确;
对于②:先求得否命题,再判断真假,结合二次不等式的解法易知其否命题为真;
对于③:A>30°,可以举一个反例否定即可;
对于④:若为奇函数,则应有f(0)=0,能否得到φ=kπ;反之当φ=kπ时,判断是否有f(-x)=f(x)即可.
解答 解:对于①:其逆命题是:如果x、y互为相反数,则x+y=0,显然正确;
对于②:否命题是“如果x2+x-6<0,则x≤2”,由x2+x-6<0得-3<x<2,此时x≤2显然不成立,故②错误;
对于③:当A=150°时,sinA=$\frac{1}{2}$,不满足结论,故③为假;
对于④:当函数f(x)=tan(x+φ)为奇函数时,结合图象可知,当x=0时,f(0)=0或不存在,则应有φ=kπ或kπ+$\frac{π}{2}$,k∈Z,故不满足充分性,故④错误.
故答案为:①.
点评 本题综合考查了命题真假的判断方法,主要侧重于基础知识考查,难度并不大.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
16.函数f(x)=$\frac{\sqrt{10+9x-{x}^{2}}}{lg(x-1)}$的定义域为( )
| A. | [1,10] | B. | [1,2)∪(2,10] | C. | (1,10] | D. | (1,2)∪(2,10] |
12.如图C是△PAB边AB内的一点,下列说法正确的是( )
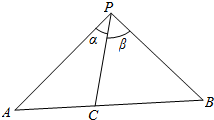

| A. | PCsin(α+β)=PBsinα+PAsinβ | B. | PCsin(α+β)=PAsinα+PBsinβ | ||
| C. | $\frac{sin(α+β)}{PC}$=$\frac{sinα}{PB}$+$\frac{sinβ}{PA}$ | D. | $\frac{sin(α+β)}{PC}$=$\frac{sinα}{PA}$+$\frac{sinβ}{PB}$ |