题目内容
15.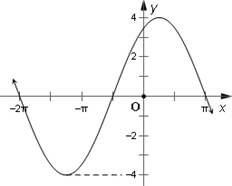 下列函数中,图象的一部分如图所示的是( )
下列函数中,图象的一部分如图所示的是( )| A. | $y=4sin(\frac{2x}{3}+\frac{π}{3})$ | B. | $y=4sin(\frac{2x}{3}-\frac{2π}{3})$ | C. | $y=4cos(\frac{2x}{3}+\frac{π}{3})$ | D. | $y=4cos(\frac{2x}{3}-\frac{2π}{3})$ |
分析 根据函数的图象,求出函数的周期,确定ω,求出A,根据图象过(π,0)求出φ,即可得到函数的解析式.
解答 解:∵由函数图象可得:A=4,T=π-(-2π)=3π,$ω=\frac{2π}{T}=\frac{2π}{3π}=\frac{2}{3}$,
∴不妨设y=4sin($\frac{2x}{3}$+φ),
∴由点(π,0)在函数图象上,可得:4sin($\frac{2π}{3}$+φ)=0,解得:$\frac{2π}{3}$+φ=kπ,k∈Z,可得:φ=kπ-$\frac{2π}{3}$,k∈Z,
∴当k=0时,φ=-$\frac{2π}{3}$,可得函数解析式为:$y=4sin(\frac{2x}{3}-\frac{2π}{3})$.
故选:B.
点评 本题考查正弦函数平移变换和最小正周期的求法、根据图象求函数解析式.考查学生的看图能力.属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
5.函数y=$\sqrt{3-x}$+lg(x+1)的定义域是( )
| A. | (-1,3) | B. | [-1,3) | C. | (-1,3] | D. | (3,+∞) |
6.甲、乙两名篮球运动员在某几场比赛中得分的成绩如下,甲:12,15,24,25,31,36,37,39,44,49,50;乙:13,14,16,23,26,27,28,33,38,39,51则甲、乙两人在这几场比赛中得分的中位数之和是( )
| A. | 63 | B. | 64 | C. | 65 | D. | 66 |
10.已知等差数列{an}中,an=-3n+1,则首项a1和公差d的值分别为( )
| A. | 1,-3 | B. | -2,-3 | C. | 2,3 | D. | -3,1 |
7.已知函数f(x)的值域是$[\frac{3}{8},\frac{4}{9}]$,则函数y=f(x)+$\sqrt{1-2f(x)}$的值域为[$\frac{7}{9},\frac{7}{8}$].
5.给出下列命题:
(1)设有一个回归方程$\stackrel{∧}{y}$=3-5x,变量x增加一个单位时,y平均增加5个单位;
(2)线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$ 必过点($\overline{x}$,$\overline{y}$);
(3)线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
(4)残差平方和越小的模型,模型拟合的效果越好;
(5)用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好.
其中正确 的命题是( )
(1)设有一个回归方程$\stackrel{∧}{y}$=3-5x,变量x增加一个单位时,y平均增加5个单位;
(2)线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$ 必过点($\overline{x}$,$\overline{y}$);
(3)线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
(4)残差平方和越小的模型,模型拟合的效果越好;
(5)用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好.
其中正确 的命题是( )
| A. | (1)(4) | B. | (2)( 4) | C. | (2)( 3)( 4) | D. | (2)( 5) |