题目内容
4.已知数列{an}的前n项和为Sn=n2+2n,则数列{an}的通项公式an=2n+1.分析 利用an+1=Sn+1-Sn计算可得an=2n+1,验证当n=1时是否成立即可.
解答 解:∵Sn=n2+2n,
∴Sn+1=(n+1)2+2(n+1),
∴an+1=Sn+1-Sn
=[(n+1)2+2(n+1)]-(n2+2n)
=2n+3,
∴an=2n+1,
又a1=S1=1+2=3满足上式,
∴数列{an}的通项公式an=2n+1,
故答案为:2n+1.
点评 本题考查求数列的通项,注意解题方法的积累,属于基础题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
14.已知lg2=a,lg3=b,则log36=( )
| A. | $\frac{a}{a+b}$ | B. | $\frac{b}{a+b}$ | C. | $\frac{a+b}{a}$ | D. | $\frac{a+b}{b}$ |
15.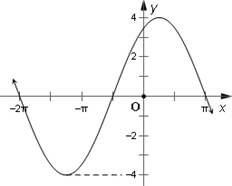 下列函数中,图象的一部分如图所示的是( )
下列函数中,图象的一部分如图所示的是( )
 下列函数中,图象的一部分如图所示的是( )
下列函数中,图象的一部分如图所示的是( )| A. | $y=4sin(\frac{2x}{3}+\frac{π}{3})$ | B. | $y=4sin(\frac{2x}{3}-\frac{2π}{3})$ | C. | $y=4cos(\frac{2x}{3}+\frac{π}{3})$ | D. | $y=4cos(\frac{2x}{3}-\frac{2π}{3})$ |
16.若ABCD是正方形,E是CD的中点,且$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,则$\overrightarrow{BE}$=( )
| A. | $\overrightarrow b+\frac{1}{2}\overrightarrow a$ | B. | $\overrightarrow b-\frac{1}{2}\overrightarrow a$ | C. | $\overrightarrow a+\frac{1}{2}\overrightarrow b$ | D. | $\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
13.已知a=-2,b=-8,则a和b的等比中项为( )
| A. | 4 | B. | -4 | C. | -5 | D. | ±4 |
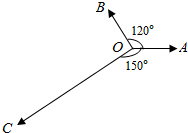 如图所示,平面内有三个向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,$\overrightarrow{OA}$与$\overrightarrow{OB}$夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$夹角为150°,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,$|{\overrightarrow{OC}}|=2\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$(λ,μ∈R),则λ+μ=( )
如图所示,平面内有三个向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,$\overrightarrow{OA}$与$\overrightarrow{OB}$夹角为120°,$\overrightarrow{OA}$与$\overrightarrow{OC}$夹角为150°,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,$|{\overrightarrow{OC}}|=2\sqrt{3}$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$(λ,μ∈R),则λ+μ=( )