题目内容
7.已知函数f(x)的值域是$[\frac{3}{8},\frac{4}{9}]$,则函数y=f(x)+$\sqrt{1-2f(x)}$的值域为[$\frac{7}{9},\frac{7}{8}$].分析 为去原函数的根号,可想着设$\sqrt{1-2f(x)}=t$,从而解出f(x)=$\frac{1-{t}^{2}}{2}$,并由f(x)的值域能得到t∈$[\frac{1}{3},\frac{1}{2}]$.将解出的f(x)带入原函数便可得到y=$-\frac{1}{2}(x-1)^{2}+1$,容易判断该函数在[$\frac{1}{3},\frac{1}{2}$]上单调递增,这样便可得出原函数的值域.
解答 解:令$\sqrt{1-2f(x)}=t$,t∈[$\frac{1}{3}$,$\frac{1}{2}$];
∴$f(x)=\frac{1-{t}^{2}}{2}$;
∴$y=\frac{1-{t}^{2}}{2}+t=-\frac{1}{2}{t}^{2}+t+\frac{1}{2}$=$-\frac{1}{2}(t-1)^{2}+1$;
该函数的对称轴为t=1;
∴该函数在[$\frac{1}{3},\frac{1}{2}$]上单调递增;
∴t=$\frac{1}{3}$时,该函数取最小值$\frac{7}{9}$,t=$\frac{1}{2}$时,该函数取最大值$\frac{7}{8}$;
∴原函数的值域为[$\frac{7}{9},\frac{7}{8}$].
故答案为:$[\frac{7}{9},\frac{7}{8}]$.
点评 考查函数值域的概念,换元求函数值域的方法,以及二次函数单调性的判断,根据单调性求函数的值域.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
18.已知向量$\overrightarrow a=(1,-m),\overrightarrow b=(m,1)$,则$\overrightarrow{a}$•$\overrightarrow{b}$=( )
| A. | -1 | B. | 0 | C. | -2m | D. | 1-m2 |
15.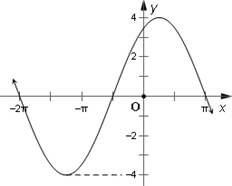 下列函数中,图象的一部分如图所示的是( )
下列函数中,图象的一部分如图所示的是( )
 下列函数中,图象的一部分如图所示的是( )
下列函数中,图象的一部分如图所示的是( )| A. | $y=4sin(\frac{2x}{3}+\frac{π}{3})$ | B. | $y=4sin(\frac{2x}{3}-\frac{2π}{3})$ | C. | $y=4cos(\frac{2x}{3}+\frac{π}{3})$ | D. | $y=4cos(\frac{2x}{3}-\frac{2π}{3})$ |
16.若ABCD是正方形,E是CD的中点,且$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,则$\overrightarrow{BE}$=( )
| A. | $\overrightarrow b+\frac{1}{2}\overrightarrow a$ | B. | $\overrightarrow b-\frac{1}{2}\overrightarrow a$ | C. | $\overrightarrow a+\frac{1}{2}\overrightarrow b$ | D. | $\overrightarrow a-\frac{1}{2}\overrightarrow b$ |