题目内容
6．甲、乙两名篮球运动员在某几场比赛中得分的成绩如下，甲：12，15，24，25，31，36，37，39，44，49，50；乙：13，14，16，23，26，27，28，33，38，39，51则甲、乙两人在这几场比赛中得分的中位数之和是（ ）| A． | 63 | B． | 64 | C． | 65 | D． | 66 |
分析 求出甲乙二人得分的中位数，再求它们的和即可．
解答 解：甲运动员的得分从小到大排列为：
12，15，24，25，31，36，37，39，44，49，50；
排在中间第6的数是36，即中位数是36；
乙运动员的得分从小到大排列为：
13，14，16，23，26，27，28，33，38，39，51；
排在中间第6的数是27，即中位数是27；
∴甲、乙两人的中位数之和是
36+27=63．
故选：A．
点评 本题考查了求数据中位数的应用问题，解题时应明确中位数的概念，是基础题目．
练习册系列答案
相关题目
14．已知lg2=a，lg3=b，则log36=（ ）
| A． | $\frac{a}{a+b}$ | B． | $\frac{b}{a+b}$ | C． | $\frac{a+b}{a}$ | D． | $\frac{a+b}{b}$ |
1．下列选项中，正确的赋值语句是（ ）
| A． | A=x2-1=（x+1）（x-1） | B． | 5=A | C． | A=A*A+A-2 | D． | 4=2+2 |
11．
已知三个正态分布密度函数φi（x）=$\frac{1}{\sqrt{2}π{σ}_{i}}$e${\;}^{-\frac{（x{μ}_{1}）^{2}}{2{σ}_{i}^{2}}}$（x∈R，i=1，2，3）的图象如图所示，则（ ）
已知三个正态分布密度函数φi（x）=$\frac{1}{\sqrt{2}π{σ}_{i}}$e${\;}^{-\frac{（x{μ}_{1}）^{2}}{2{σ}_{i}^{2}}}$（x∈R，i=1，2，3）的图象如图所示，则（ ）| A． | μ1＜μ2=μ3，σ1=σ2＞σ3 | B． | μ1＞μ2=μ3，σ1=σ2＜σ3 | ||
| C． | μ1=μ2＜μ3，σ1＜σ2=σ3 | D． | μ1＜μ2=μ3，σ1=σ2＜σ3 |
18．已知向量$\overrightarrow a=（1，-m），\overrightarrow b=（m，1）$，则$\overrightarrow{a}$•$\overrightarrow{b}$=（ ）
| A． | -1 | B． | 0 | C． | -2m | D． | 1-m2 |
15．
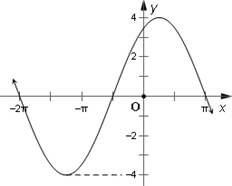下列函数中，图象的一部分如图所示的是（ ）
下列函数中，图象的一部分如图所示的是（ ）| A． | $y=4sin（\frac{2x}{3}+\frac{π}{3}）$ | B． | $y=4sin（\frac{2x}{3}-\frac{2π}{3}）$ | C． | $y=4cos（\frac{2x}{3}+\frac{π}{3}）$ | D． | $y=4cos（\frac{2x}{3}-\frac{2π}{3}）$ |
16．若ABCD是正方形，E是CD的中点，且$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AD}=\overrightarrow b$，则$\overrightarrow{BE}$=（ ）
| A． | $\overrightarrow b+\frac{1}{2}\overrightarrow a$ | B． | $\overrightarrow b-\frac{1}{2}\overrightarrow a$ | C． | $\overrightarrow a+\frac{1}{2}\overrightarrow b$ | D． | $\overrightarrow a-\frac{1}{2}\overrightarrow b$ |