题目内容
20．已知物体的运动方程为s=t2+$\frac{3}{t}$+lnt-1（t是时间，s是位移），则物体在时刻t=3时的速度为6．分析 根据位移的导数是速度，求出s的导函数即速度与时间的函数，将2代入求出物体在时刻t=3时的速度．
解答 解：物体的运动速度为v（t）=s′=2t-$\frac{3}{{t}^{2}}$+$\frac{1}{t}$
所以物体在时刻t=3时的速度为v（3）=2×3-$\frac{3}{9}$+$\frac{1}{3}$=6，
故答案为：6．
点评 本题考查导数在物理上的应用：对物体位移求导得到物体的瞬时速度．
练习册系列答案
相关题目
11．
已知三个正态分布密度函数φi（x）=$\frac{1}{\sqrt{2}π{σ}_{i}}$e${\;}^{-\frac{（x{μ}_{1}）^{2}}{2{σ}_{i}^{2}}}$（x∈R，i=1，2，3）的图象如图所示，则（ ）
已知三个正态分布密度函数φi（x）=$\frac{1}{\sqrt{2}π{σ}_{i}}$e${\;}^{-\frac{（x{μ}_{1}）^{2}}{2{σ}_{i}^{2}}}$（x∈R，i=1，2，3）的图象如图所示，则（ ）| A． | μ1＜μ2=μ3，σ1=σ2＞σ3 | B． | μ1＞μ2=μ3，σ1=σ2＜σ3 | ||
| C． | μ1=μ2＜μ3，σ1＜σ2=σ3 | D． | μ1＜μ2=μ3，σ1=σ2＜σ3 |
15．
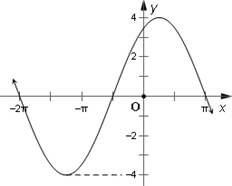下列函数中，图象的一部分如图所示的是（ ）
下列函数中，图象的一部分如图所示的是（ ）| A． | $y=4sin（\frac{2x}{3}+\frac{π}{3}）$ | B． | $y=4sin（\frac{2x}{3}-\frac{2π}{3}）$ | C． | $y=4cos（\frac{2x}{3}+\frac{π}{3}）$ | D． | $y=4cos（\frac{2x}{3}-\frac{2π}{3}）$ |