题目内容
5．给出下列命题：（1）设有一个回归方程$\stackrel{∧}{y}$=3-5x，变量x增加一个单位时，y平均增加5个单位；
（2）线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$ 必过点（$\overline{x}$，$\overline{y}$）；
（3）线性相关系数r越大，两个变量的线性相关性越强；反之，线性相关性越弱；
（4）残差平方和越小的模型，模型拟合的效果越好；
（5）用相关指数R2来刻画回归效果，R2越小，说明模型的拟合效果越好．
其中正确 的命题是（ ）
| A． | （1）（4） | B． | （2）（ 4） | C． | （2）（ 3）（ 4） | D． | （2）（ 5） |
分析 （1）回归方程$\stackrel{∧}{y}$=3-5x时，变量x增加一个单位，y平均减少5个单位；
（2）线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$过样本中心点（$\overline{x}$，$\overline{y}$）；
（3）线性相关系数|r|越接近1，两个变量的线性相关性越强；
（4）残差平方和越小的模型，模型拟合的效果就越好；
（5）用相关指数R2来刻画回归效果时，R2越大，模型的拟合效果越好．
解答 解：对于（1），当回归方程为$\stackrel{∧}{y}$=3-5x时，变量x增加一个单位，y平均减少5个单位，
∴命题（1）错误；
对于（2），线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$过样本中心点（$\overline{x}$，$\overline{y}$），
∴命题（2）正确；
对于（3），线性相关系数|r|越大，两个变量的线性相关性越强；反之，线性相关性越弱，
∴命题（3）错误；
对于（4），残差平方和越小的模型，模型拟合的效果就越好，反之，模型拟合的效果就越差，
∴命题（4）正确；
对于（5），用相关指数R2来刻画回归效果，R2越大，说明模型的拟合效果越好，
∴命题（5）错误；
综上，正确的命题是（2）、（4）．
故选：B．
点评 本题考查了回归分析的应用问题，也考查了线性相关系数、残差以及相关指数的应用问题，是基础题目．
练习册系列答案
相关题目
15．
下列函数中，图象的一部分如图所示的是（ ）
下列函数中，图象的一部分如图所示的是（ ）| A． | $y=4sin（\frac{2x}{3}+\frac{π}{3}）$ | B． | $y=4sin（\frac{2x}{3}-\frac{2π}{3}）$ | C． | $y=4cos（\frac{2x}{3}+\frac{π}{3}）$ | D． | $y=4cos（\frac{2x}{3}-\frac{2π}{3}）$ |
16．若ABCD是正方形，E是CD的中点，且$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AD}=\overrightarrow b$，则$\overrightarrow{BE}$=（ ）
| A． | $\overrightarrow b+\frac{1}{2}\overrightarrow a$ | B． | $\overrightarrow b-\frac{1}{2}\overrightarrow a$ | C． | $\overrightarrow a+\frac{1}{2}\overrightarrow b$ | D． | $\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
13．已知a=-2，b=-8，则a和b的等比中项为（ ）
| A． | 4 | B． | -4 | C． | -5 | D． | ±4 |
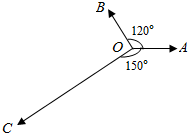如图所示，平面内有三个向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$，$\overrightarrow{OA}$与$\overrightarrow{OB}$夹角为120°，$\overrightarrow{OA}$与$\overrightarrow{OC}$夹角为150°，且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$，$|{\overrightarrow{OC}}|=2\sqrt{3}$，若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$（λ，μ∈R），则λ+μ=（ ）