题目内容
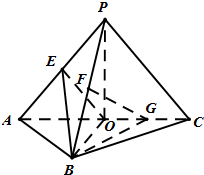
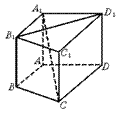
如图，三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC，∠ACB=90°，E是棱CC1上动点，F是AB中点，AC=1，BC=2，AA1=4．
（1）当E是棱CC1中点时，求证：CF∥平面AEB1；
（2）在棱CC1上是否存在点E，使得二面角A-EB1-B的余弦值是
，若存在，求CE的长，若不存在，请说明理由．
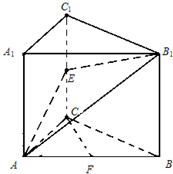
（1）当E是棱CC1中点时，求证：CF∥平面AEB1；
（2）在棱CC1上是否存在点E，使得二面角A-EB1-B的余弦值是
2
| ||
| 17 |
（1）证明：取AB1的中点G，联结EG，FG
∵F、G分别是棱AB、AB1中点，∴FG∥BB1，FG=
BB1
又∵FG∥EC，EC=
CC1，FG=EC，∴四边形FGEC是平行四边形，
∴CF∥EG．
∵CF?平面AEB1，EG?平面AEB1，
∴CF∥平面AEB；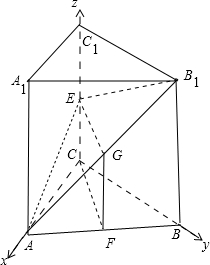
（2）以C为坐标原点，射线CA，CB，CC1为x，y，z轴正半轴，
建立如图所示的空间直角坐标系C-xyz
则C（0，0，0），A（1，0，0），B1（0，2，4）
设E（0，0，m）（0≤m≤4），平面AEB1的法向量
=(x，y，z)
=(-1，2，4)，
=(-1，0，m)．
由
，得
，取z=2，得
=(2m，m-4，2)
∵CA⊥平面C1CBB1，
∴
是平面EBB1的法向量，则平面EBB1的法向量
=
=(1，0，0)
∵二面角A-EB1-B的平面角余弦值为
，
则cos＜
，
＞=
=
=
，解得m=1（0≤m≤4）．
∴在棱CC1上存在点E，符合题意，此时CE=1．
∵F、G分别是棱AB、AB1中点，∴FG∥BB1，FG=
| 1 |
| 2 |
又∵FG∥EC，EC=
| 1 |
| 2 |
∴CF∥EG．
∵CF?平面AEB1，EG?平面AEB1，
∴CF∥平面AEB；
（2）以C为坐标原点，射线CA，CB，CC1为x，y，z轴正半轴，
建立如图所示的空间直角坐标系C-xyz
则C（0，0，0），A（1，0，0），B1（0，2，4）
设E（0，0，m）（0≤m≤4），平面AEB1的法向量
| n1 |
| AB1 |
| AE |
由
|
|
| n1 |
∵CA⊥平面C1CBB1，
∴
| CA |
| n2 |
| CA |
∵二面角A-EB1-B的平面角余弦值为
2
| ||
| 17 |
则cos＜
| n1 |
| n2 |
| ||||
|
|
| 2m | ||
|
2
| ||
| 17 |
∴在棱CC1上存在点E，符合题意，此时CE=1．
练习册系列答案
相关题目
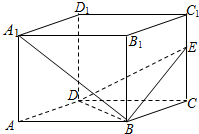
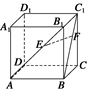且B1E=C1F.求证：EF∥平面ABCD.
